At $t = 0$, a particle starts from rest and moves along a straight line, whose acceleration-time graph is shown in the figure.

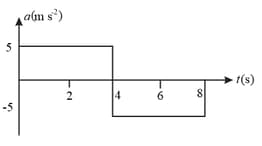
Convert this graph into a velocity-time graph. From the velocity-time graph, find the maximum velocity attained by the particle. Also, find from, $v-t$ graph, the displacement and distance travelled by the particle from $2$ to $6 \mathrm{s}$.

The figure shows the position-time graphs of three cars $A$, $B$ and $C$. On the basis of the graphs, answer the following questions.

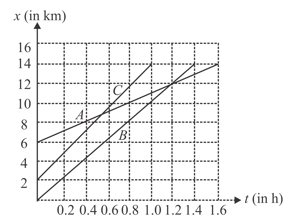
(a) Which car has the highest speed and which has the lowest?
(b) Are the three cars ever at the same point on the road?
(c) When $C$ passes $A$, where is $B$?
(d) What is the time interval during car $A$ travel between the time it passed cars $B$ and $C$?
(e) What is the relative velocity of car $C$ with respect to car $A$?
(f) What is the relative velocity of car $B$ with respect to car $C$?

A car accelerates from rest at a constant rate $\alpha$ for some time after which it decelerates at a constant rate of $\beta$ to come to rest. If the total time elapsed is $t \sec$, then calculate,

(a) the maximum velocity attained by the car, and

(b) the total displacement travelled by the car in terms of $\alpha \text{,} \beta$ and $t$.

Two cars $A$ and $B$, move along the $x\text{-}$axis. Car $A$ starts from rest with constant acceleration while car $B$ moves with constant velocity.

(a) At what time in $\sec \text{,} t\left(\mathrm{s}\right)$, if any, $A$ and $B$ have the same position?

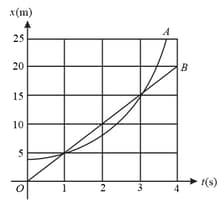
(b) At what time $\left(\mathrm{s}\right)$, if any, do $A$ and $B$ have the same velocity? What is the velocity of car $B$ at this time?
(c) Graph velocity versus time for both $A$ and $B$.
(d) At what time $\left(\mathrm{s}\right)$, if any, does car $A$ pass car $B$?
(e) At what time $\left(\mathrm{s}\right)$, if any, does car $B$ pass car $A$?

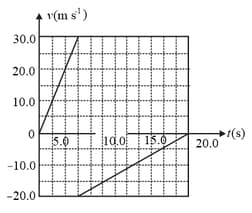
A rigid ball travelling in a straight line (the $x$-axis) hits a solid wall and suddenly rebounds during a brief instant. The $v_{\mathrm{x}}\text{-}t$ graph in figure shows this ball's velocity as a function of time. During the first $20 \mathrm{s}$ of its motion, find,

(a) its displacement,

(b) the total distance the ball moves, and

(c) sketch a graph of $a_{\mathrm{x}}\text{-}t$ for this ball's motion.

(d) Is the graph shown really vertical at $5 \mathrm{s}$? Explain.

Referring the $v\text{-}s$ diagram given below, find,

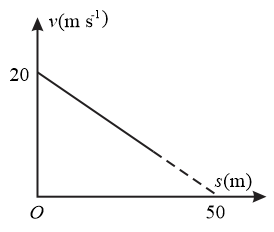
(a) the acceleration of the particle when its velocity becomes half of the initial velocity,

(b) the total distance covered by the particle.

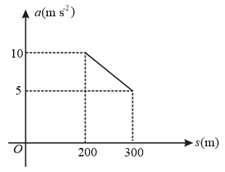
A racing motor boat speeds up in a straight line in a lake from rest. Referring to the acceleration-displacement graph for the speeding boat, find its speed when it passes a raft at a distance of $40 \mathrm{m}$ from the starting point.

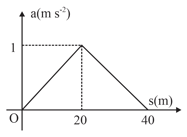
Referring $a\text{-}s$ diagram in figure, find the velocity after a particle travels $250 \mathrm{m}$ from starting. Assume $v_0=0$.