Can two equilateral triangles always be congruent? Give reasons.
Important Questions on Justification
In the given figure,. Prove that . Is ?
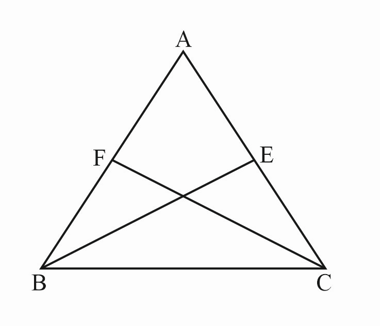
In the given figure, is isosceles in which . If and are the midpoints of and respectively. Prove that .
In the given figure, . Prove and hence show that and .
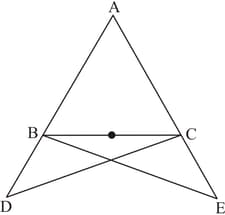
In the given figure, is isosceles in which . If and are produced to and respectively such that . Prove that .
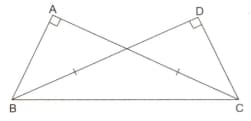
In the given figure, triangles are right-angled at and respectively and . Prove that .
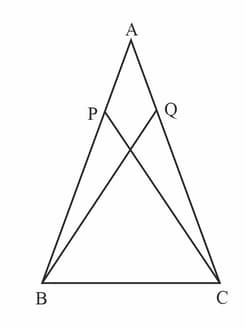
In the given figure, and are two points on equal sides and of an isosceles triangle such that . Prove that .
In the given figure, is a triangle in which is the bisector of . If , show that is isosceles.
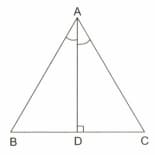
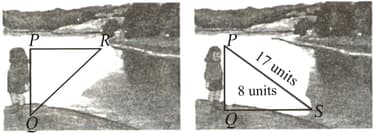
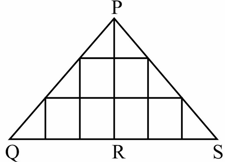
From the above description, find the value of .
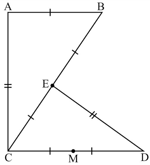
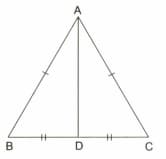
In the given figure, is an isosceles triangle in which . Also, is a point such that . Prove that bisects and .
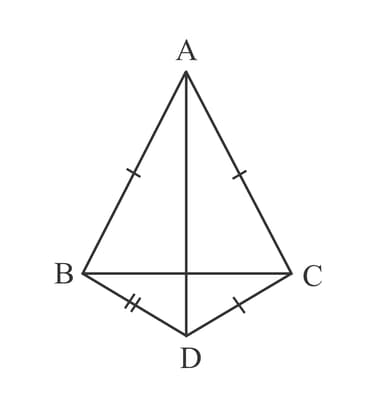
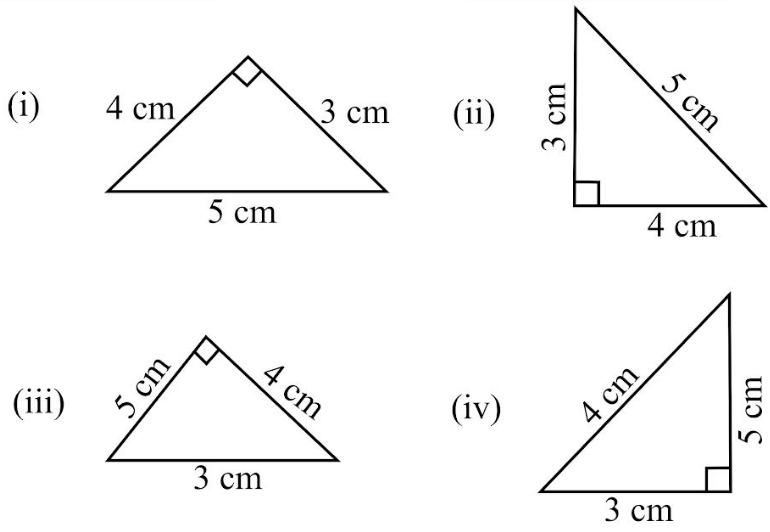
In the given figure, and . Is ? Give reasons in support of your answer.
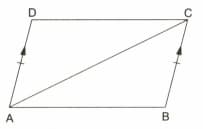
In the given figure, . Prove that .



