Consider a parallelogram ABCD. Fill the blanks to find the type of parallelogram obtained if the diagonals of the parallelogram are equal.

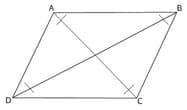
In ∆ ABC and ∆ ABD,

AB is the common side.

AC = BD (Diagonals are equal)

AD = BC (Opposite sides of a parallelogram are equal)

∴ By SSS rule of congruency, the ∆ ABC and ∆ ABD are congruent.

∠ DAB = ∠ CBA (By CPCT)

Similarly,

∠ CDA = ∠ DCB

But ∠ DAB + ∠ CBA = 180 degrees (Co interior angles of parallel lines are supplementary)

∴ ABCD is a .

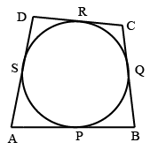
A circle is inscribed in quadrilateral ABCD, touching sides AB, BC, CD and DA at P, Q,R and S, respectively. If $\mathrm{As}=6\mathrm{cm},$ $\mathrm{BC}=12\mathrm{cm}$ and $\mathrm{CR}=5\mathrm{cm}$, then the length of AB (in cm) is

In the figure given below, a rectangle of perimeter $76$ units is divided into $7$ congruent rectangles:

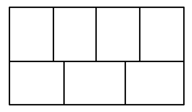
What is the perimeter of each of the smaller rectangles?

$5 : 18$ is the ratio of the length and perimeter of a rectangle. What would be the ratio of its length and breadth?

What is the area of this trapezoidal garden (All measurements are in cm)? 

1. $60$ sq.cm
2. $180$ sq.cm
3. $210$ sq.cm 
4. $240$ sq.cm

How many quadrilaterals are there in the given figure?