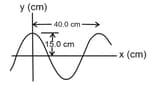
Consider a sinusoidal travelling wave shown in the figure. The wave velocity is $+40 \mathrm{cm} {\mathrm{s}}^{-1}$.

Find,

(a) the frequency
(b) the phase difference between points which are $2.5 \mathrm{cm}$ apart.
(c) how long it takes for the phase at a given position to change by $60°$.
(d) the velocity of a particle at point $P$ at the instant shown.

The equation of a travelling wave is, $y(x,t)=0.02\sin \left(\frac{x}{0.05}+\frac{t}{0.01}\right)\mathrm{m}$.
Find,
(a) the wave velocity and
(b) the particle velocity at $x=0.2 \mathrm{m}$ and $t=0.3 \mathrm{s}$.
Given, $\cos \left(\mathrm{\theta }\right)=-0.85$ where, $\mathrm{\theta }=34 \mathrm{rad}$.

Transverse waves on a string have wave speed $12.0 \mathrm{m} {\mathrm{s}}^{-1}$, amplitude $0.05 \mathrm{m}$ and wavelength $0.4 \mathrm{m}$. The waves travel in the $X-$direction and at $t=0$, the $x=0$ end of the string has zero displacement and is moving upwards.

(a) Write a wave function describing the wave.
(b) Find the transverse displacement of a point at $x=0.25 \mathrm{m}$ at time, $t=0.15 \mathrm{s}$.
(c) How much time must elapse from the instant in part (b) until the point at $x=0.25$ $\mathrm{m}$ has zero displacement?

A wave is described by the equation, $y=(1.0 \mathrm{mm})\mathrm{sin\pi }\left(\frac{x}{2.0 \mathrm{cm}}-\frac{t}{0.01 \mathrm{s}}\right)$.

(a) Find the time period and wavelength.
(b) Write the equation for the velocity of the particles. Find the speed of the particle at $x=1.0 \mathrm{cm}$ at time $t=0.01 \mathrm{s}$.
(c) What are the speeds of the particles at $x=3.0 \mathrm{cm}, 5.0 \mathrm{cm}$ and $7.0 \mathrm{cm}$ at $t=0.01 \mathrm{s}$?
(d) What are the speeds of the particles at $x=1.0 \mathrm{cm}$ at $t=0.011 \mathrm{s}, 0.012 \mathrm{s}$ and $0.013 \mathrm{s}$?

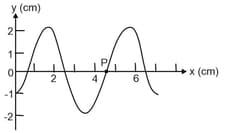
A sinusoidal wave traveling in the positive $x$-direction has an amplitude of $15.0 \mathrm{cm}$, a wavelength of $40.0 \mathrm{cm}$ and a frequency of $8.00 \mathrm{Hz}$. The vertical displacement of the medium at $t=0$ and $x=0$ is also $15.0 \mathrm{cm}$ as shown in figure.

(a) Find the angular wave number $k$, period $T$, angular frequency $\mathrm{\omega }$ and speed $v$ of the wave.
(b) Write a general expression for the wave function.

A flexible steel cable of total length $L$ and mass per unit length $\mathrm{\mu }$ hangs vertically from a support at one end.

(a) Show that the speed of a transverse wave down the cable is, $v=\sqrt{g(L-x)}$ where, $x$ is measured from the support.

(b) How long will it take for a wave to travel down the cable?

A loop of rope is whirled at a high angular velocity $\omega$ so that it becomes a taut circle of radius $R$. A kink develops in the whirling rope.

(a) Show that the speed of the kink in the rope is, $v=\omega R$.
(b) Under what conditions does the kink remain stationary relative to an observer on the ground?