Consider a string with both ends fixed. A standing wave in the second harmonic mode is established on the string, as shown in the diagram. The speed of wave is $180 \mathrm{m} {\mathrm{s}}^{-1}$.

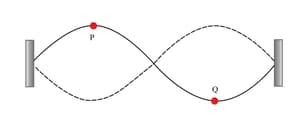
Consider the vibrations of two points on the string, P and Q. The displacement of point P is given by the equation $y=5.0 \cos \left(45\pi t\right)$ where $y$in $\mathrm{mm}$ and $t$is in seconds. Calculate the length of the string.

Consider a string with both ends fixed. A standing wave in the second harmonic mode is established on the string, as shown in the diagram.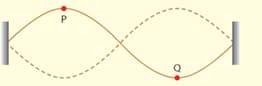

Consider the vibrations of two points on the string, P and Q. The displacement of point P is given by the equation $y=5.0 \cos \left(45\pi t\right)$ where $y$in $\mathrm{mm}$ and $t$is in seconds. State the phase difference between the oscillation of point P and that of point Q. Hence write down the equation giving the displacement of point Q.

A horizontal aluminium rod of length $1.2 \mathrm{m}$ is hit sharply with a hammer. The hammer rebounds from the rod $0.18 ms$ later. Explain why the hammer rebounds.

A horizontal aluminium rod of length $1.2 \mathrm{m}$ is hit sharply with a hammer. The hammer rebounds from the rod $0.18 \mathrm{ms}$ later. Calculate the speed of sound in aluminium.

A horizontal aluminium rod of length $1.2 \mathrm{m}$ is hit sharply with a hammer. The hammer rebounds from the rod $0.18 \mathrm{ms}$ later. Calculate the speed of sound in aluminium. The hammer created a longitudinal standing wave in the rod. Estimate the frequency of the sound wave by assuming that the rod vibrates in the first harmonic.

The diagram shows a print P on a string at a particular instant of time. A transverse wave is travelling along the string from left to right.

Which is correct about the direction and the magnitude of the velocity of point P at this instant?

The graph shows the displacement of a medium when a longitudinal wave travels through the medium from left to right. Positive displacements correspond to motion to the right. Which point corresponds to the centre of the compression?