Consider interference between two sources of intensity $I$ and $4I$. Find out resultant intensity where phase difference is $4\pi$

Express all your answers in the form $nI$ where $n$ is real number up to two decimal places. Find $n$.

A ray of light of intensity I is incident on a parallel glass-slab at a point $A$ as shown in figure. It undergoes partial reflection and refraction. At each reflection $20\%$ of incident energy is refracted. The rays $AB$ and $A^{\text{'}}{B}^{\text{'}}$ undergo interference. The ratio of $\frac{I_{\max }}{I_{\min }}$ is $x:1$. Write the value of $x$.

A thin glass plate of thickness $t$ and refractive index $\mu$ is inserted between screen and one of the slits in a Young's experiment. If the intensity at the centre of the screen is $I$, what was the intensity at the same point prior to the introduction of the sheet.
Express your answer as $I{\cos }^2\left[\frac{k(\mu -1)t}{\lambda }\right]$ and find the value of $k$.

(Take $\pi =3.14$)

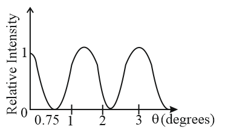
Light of wavelength $520 \mathrm{nm}$ passing through a double slit, produces interference pattern of relative intensity versus deflection angle $\theta$ as shown in the figure. Find the separation $d$ between the slits. If your answer is $x\times {10}^{-2} \mathrm{mm}$, fill the value of $x$.

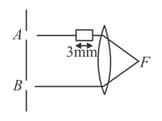
Two identical monochromatic light sources $A\&B$ intensity ${10}^{-15} \mathrm{W} {\mathrm{m}}^2$ produce wavelength of light $4000\sqrt{3} \stackrel{°}{\mathrm{A}}$. A glass of thickness $3 \mathrm{mm}$ is placed in the path of the ray as shown in figure. The glass has a variable refractive index $n=1+\sqrt{x}$ where $x$ (in mm) is distance of plate from left to right. Calculate total intensity at focal point $F$ of the lens.

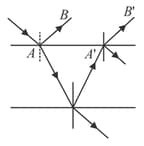
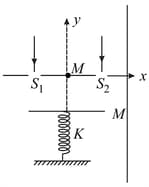
Two slits $S_1$ and $S_2$ on the $x$-axis and symmetric with respect to y-axis are illuminated by a parallel monochromatic light beam of wavelength $\lambda$. The distance between the slits is $d(>>\lambda )$. Point $M$ is the mid point of the line $S_1{ S}_2$ and this point is considered as the origin. The slits are in horizontal plane. The interference patten is observed on a horizontal plate (acting as screen) of mass $M$, which is attached to one end of a vertical spring of spring constant $K$. The other end of the spring is fixed to ground. At $t=0$ the plate is at a distance $D(>>d)$ below the plane of slits and the spring is in its natural length. The plate is left from rest from its initial position. Find the $x$ and $y$ co-ordinates of the $n^{th }$  maxima on the plate as a function of time. Assume that spring is light and plate always remains horizontal.

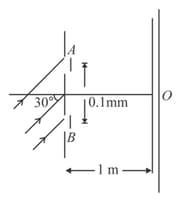
In a YDSE a parallel beam of light of wavelength $6000\stackrel{°}{\mathrm{A}}$ is incident on slits at angle of incidence $30°$. $A$ and $B$ are two thin transparent films each of refractive index $1.5$. Thickness of $A$ is $20.4 \mathrm{\mu m}$. Light coming through $A$ and $B$ have intensities $I$ and $4I$ respectively on the screen. Intensity at point $O$ which is symmetric relative to the slits is $3I$. The central maxima is above $O$.
(i) What is the maximum thickness of $B$ to do so.  Assuming thickness of $B$ to be that found in part (i) answer the following parts.

(ii) Find fringe width, maximum intensity and minimum intensity on screen.

(iii) Distance of the nearest minima from $O$.

(iv) Intensity at $5 \mathrm{cm}$ on either side of $O$.