Deduce that a satellite orbiting a planet of mass in a circular orbit of the radius has a period of revolution given by
.

Important Questions on Fields (HL)
Two stars of equal masses orbit a common mass as shown in the diagram. The radius of orbit of each star is . Assume that each star has a mass equal to ( solar mass= ) and the initial separation of the star is .
State the magnitude of the force on each star in terms of .
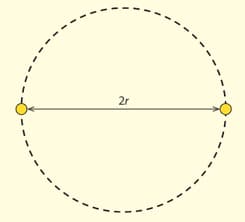
Two stars of equal mass orbit a common mass as shown in the diagram. The radius of orbit of each star is .
Deduce that the period of revolution of each star is given by
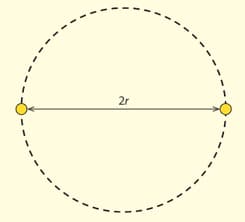
Two stars of equal mass orbit a common mass as shown in the diagram. The radius of orbit of each star is . Assume that each star has a mass equal to (solar mass= ) and the initial separation of the star is .
Deduce that the period of revolution of each star is given by
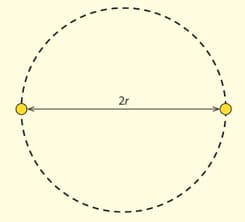
Evaluate the period numerically
