A particle of mass m is moving along the side of a square of side 'a', with a uniform speed υ in the x-y plane as shown in the figure: Which of the following statements is false for the angular momentum L → about the origin?

L → = m υ 2 R k ^ when the particle is moving from D to A.

L → = m υ R 2 + a k ^ when the particle is moving from B to C.

L → = - m υ 2 R k ^ when the particle is moving from A to B.

L → = m υ R 2 + a k ^ when the particle is moving from C to D.

MEDIUM

Earn 100

Define angular momentum. What is its physical significance ?

Important Questions on Systems of Particles and Rotational Motion

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

In a physical balance working on the principle of moments, when

5 mg

weight is placed on the left pan, the beam becomes horizontal. Both the empty pans of the balance are of equal mass. Which of the following statements is correct?

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A solid sphere is rotating freely about its symmetric axis in free space. The radius of the sphere is increased keeping its mass same. Which of the following physical quantities would remain constant for the sphere?

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A thin circular ring of mass

m

and radius

R

is rotating about its axis perpendicular to the plane of the ring with a constant angular velocity

ω

. Two point particles each of mass

M

are attached gently to the opposite ends of a diameter of the ring. The ring now rotates, with an angular velocity

\frac{ω}{2}

. Then, the ratio

\frac{m}{M}

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A particle of mass m is moving along the side of a square of side 'a', with a uniform speed

υ

in the x-y plane as shown in the figure:

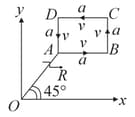
Question Image

Which of the following statements is false for the angular momentum

\vec{L}

about the origin?

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A hoop of radius

r

and mass

m

rotating with an angular velocity

ω_{0}

is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A ball of mass

160 g

is thrown up at an angle of

60 °

to the horizontal at a speed of

10 m s^{- 1}

. The angular momentum of the ball at the highest point of the trajectory with respect to the point from which the ball is thrown is nearly

(g = 10 m s^{- 2})

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A disc of the moment of inertia

I_{1}

is rotating in a horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed

ω_{1}

Another disc of the moment of inertia

I_{2}

having zero angular speed is placed coaxially on a rotating disc. Now both the disc are rotating with the constant angular speed

ω_{2}

. The energy lost by the initial rotating disc is

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

Two coaxial discs, having moments of inertia

I_{1}

and

\frac{I_{1}}{2}

, are rotating with respective angular velocities

ω_{1}

and

\frac{ω_{1}}{2}

(in the same direction), about their common axis. They are brought in contact with each other and thereafter they rotate with a common angular velocity. If

E_{f}

and

E_{i}

are the final and initial total energies, then

(E_{f} - E_{i})

is:

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A particle of mass $2 kg$ is on a smooth horizontal table and moves in a circular path of radius $0.6 m$ . The height of the table from the ground is $0.8 m$ . If the angular speed of the particle is $12 rad s^{- 1}$ , the magnitude of its angular momentum about a point on the ground right under the center of the circle is:

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A bob of mass m attached to an inextensible string of length

l

is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed

ω

rad/s about the vertical. About the point of suspension :

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A ring of mass

M

and radius

R

is rotating with angular speed

ω

about a fixed vertical axis passing through its centre O with two point masses each of mass

\frac{M}{8}

at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is

\frac{8}{9} ω

and one of the masses is at a distance of

\frac{3}{5} R

from O. At this instant the distance of the other mass from O is

Question Image

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A particle of mass

20 g

is released with an initial velocity

5 m s^{- 1}

along the curve from the point

A,

as shown in the figure. The point

A

is at height

h

from point

B .

The particle slides along the frictionless surface. When the particle reaches point

B,

its angular momentum about

O

will be: (Take

g = 10 m s^{- 2}

)

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A cubical block of side $30 cm$ is moving with velocity $2 m s^{- 1}$ on a smooth horizontal surface. The surface has a bump at a point $O$ as shown in the figure. The angular velocity (in rad/s) of the block immediately after it hits the bump, is :

Question Image

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A horizontal disk of moment of inertia

4.25 kg - m^{2}

with respect to its axis of symmetry is spinning counter clockwise at

15

revolutions per second about its axis, as viewed from above. A second disk of moment of inertia

1.80 kg - m^{2}

with respect to its axis of symmetry is spinning clockwise at

25

revolutions per second as viewed from above about the same axis and is dropped on top of the first disk. The two disks stick together and rotate as one about their axis of symmetry. The new angular velocity of the system as viewed from above is close to.

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

The time dependence of the position of a particle of mass

m = 2

is given by

\vec{r} (t) = 2 t \hat{i} - 3 t^{2} \hat{j}

. Its angular momentum, with respect to the origin, at time

t = 2

is:

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

Three point masses each of mass

m

are kept at the corners of an equilateral triangle of side

L

. The system rotates about the center of the triangle without any change in the separation of masses during rotation. The period of rotation is directly proportional to

(\cos 30 ° = s i n 60 ° = \frac{\sqrt{3}}{2})

MEDIUM

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A thin smooth rod of length

L

and mass

M

is rotating freely with angular speed

ω_{0}

about an axis perpendicular to the rod and passing through center. Two beads of mass

m

and negligible size are at the center of the rod initially. The beads of mass

m

and negligible size are at the center of the rod initially. The beads are free to slide along the rod. The angular speed of the system, when the beads reach the opposite ends of the rod, will be:

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

Two rotating bodies,

A

and

B

of masses,

m

and

2 m

with moments of inertia

I_{A}

and

I_{B} (I_{B} > I_{A})

have equal kinetic energy of rotation. If,

L_{A}

and

L_{B}

be their angular momenta, respectively, then,

EASY

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

A force

\vec{F} = α \hat{i} + 3 \hat{j} + 6 \hat{k}

is acting at a point

\vec{r} = 2 \hat{i} - 6 \hat{j} - 12 \hat{k}

. The value of

α

for which angular momentum about origin is conserved is:

HARD

Physics>Mechanics>Systems of Particles and Rotational Motion>Torque

Two thin circular discs of mass $m$ and $4 m$ , having radii of $a$ and $2 a$ , respectively, are rigidly fixed by a massless, right rod of length $l = \sqrt{24} a$ through their center. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is $ω$ . The angular momentum of the entire assembly about the point $O$ is $\vec{L}$ (see the figure). Which of the following statement(s) is(are) true?

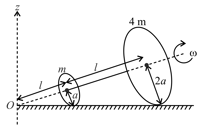
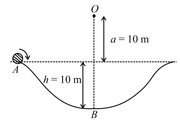
Question Image

Define angular momentum. What is its physical significance ?

Important Questions on Systems of Particles and Rotational Motion

Learn and Prepare for any exam you want !