Define viscosity and coefficient of viscosity. Write SI unit and dimensional formula of coefficient of viscosity.

The platelets are drifting with the blood flowing in a streamline flow through a horizontal artery as shown below:

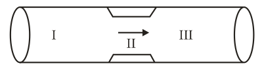
Artery is contracted in region $\mathrm{II}$. Choose the correct statement.

What will be the nature of flow of water from a circular tap, when its flow rate increased from $0.18 \mathrm{L} {\left(\min \right)}^{-1}$ to $0.48 \mathrm{L} {\left(\min \right)}^{-1}?$ The radius of the tap and viscosity of water are $0.5 \mathrm{cm}$ and ${10}^{-3} \mathrm{Pa} \mathrm{s}$, respectively. (Density of water : ${10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$)

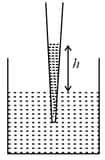
Consider the configuration of a stationary water tank of cross-section area $A_0$ and a small bucket as shown in figure below;

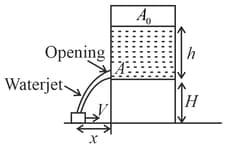
What should be the speed $v$ of the bucket, so that the water leaking out of a hole of cross-section area $A$ (as shown) from the water tank does not fall outside the bucket?

(Take, $h=5 \mathrm{m}, H=5 \mathrm{m}, \mathrm{g}=10 \mathrm{m} {\mathrm{s}}^{-2}, A=5 {\mathrm{cm}}^2$ and $A_0=500 {\mathrm{cm}}^2$).

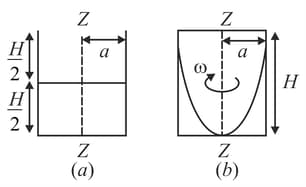
A cylinder of radius $a$ and height $H$ is filled with a liquid to an unknown height $h.$ When it is rotated at an unknown constant angular velocity $\omega ,$ the base of the cylinder gets exposed when the liquid just starts spilling out, as shown in figure.
(a) Find the height $h$ of the liquid.
(b) Find the angular speed $\omega$ of the cylinder.

Consider the following statements:

1. Taking into account, the fact that any object which floats must have an average density less than that of water during World War 1, a number of cargo vessels were made of concrete.

2. Concrete cargo vessels were filled with air.

3. A ship floats higher in the water on a high-pressure day than on a low-pressure day.

4. Floating of the ship in the water is not possible because of the buoyancy force which is present due to pressure difference.

Which of the statements given above are correct?