Match the following: (where R is gas constant) Column I Column II (a) Molar specific heat of helium gas at constant volume (i) 3 R (b) Molar specific heat of oxygen at constant volume (ii) 3 . 5 R (c) Molar specific heat of carbon dioxide at constant volume (iii) 1 . 5 R (d) Molar specific heat of hydrogen at constant pressure (iv) 2 . 5 R

( a - iii ) , ( b - iv ) , ( c - i ) , ( d - ii )

( a - i ) , ( b - ii ) , ( c - iii ) , ( d - iv )

( a - ii ) , ( b - ii ) , ( c - iv ) , ( d - i )

( a - iv ) , ( b - i ) , ( c - ii ) , ( d - iii )

MEDIUM

Earn 100

Derive the formula for the molar specific heat capacity at constant volume of a mixture of two gases.

Important Questions on Molecular Properties of Matter

MEDIUM

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

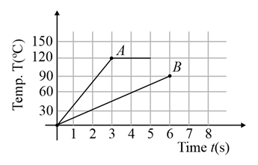
Two different metal bodies $A$ and $B$ of equal mass are heated at a uniform rate under similar conditions. The variation of temperature of the bodies is graphically represented as shown in the figure. The ratio of specific heat capacities is:

Question Image

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

The values of

C_{p}

and

C_{v}

for a diatomic gas are respectively

(R = g a s

constant)

MEDIUM

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

The correct relation between the degrees of freedom

f

and the ratio of specific heat

γ

is:

MEDIUM

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

Match the following: (where $R$ is gas constant)

	Column I		Column II
(a)	Molar specific heat of helium gas at constant volume	(i)	$3 R$
(b)	Molar specific heat of oxygen at constant volume	(ii)	$3.5 R$
(c)	Molar specific heat of carbon dioxide at constant volume	(iii)	$1.5 R$
(d)	Molar specific heat of hydrogen at constant pressure	(iv)	$2.5 R$

HARD

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

The specific heats,

C_{p}

and

C_{v}

of a gas of diatomic molecules,

A,

are given (in units of

J m o l^{- 1} K^{- 1}

) by

29

and

22,

respectively. Another gas of diatomic molecules,

B,

has the corresponding values

30

and

21 .

If they are treated as ideal gases, then:

HARD

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

For a monoatomic ideal gas following the cyclic process $A B C A$ shown in the $U$ vs $ρ$ plot, identify the incorrect option:

Question Image

MEDIUM

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

One mole of a monoatomic ideal gas undergoes a quasistatic process, which is depicted by a straight line joining points

(V_{0}, T_{0})

and

(2 V_{0}, 3 T_{0})

in a

V - T

diagram. What is the value of the heat capacity of the gas at the point

(V_{0}, T_{0}) ?

MEDIUM

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

The ratio of specific heats

(\frac{C_{P}}{C_{V}})

in terms of degree of freedom

(f)

is given by :

HARD

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

Consider a mixture of

n

moles of helium gas and

2 n

moles of oxygen gas (molecules taken to be rigid) as an ideal gas. Its

\frac{C_{P}}{C_{V}}

value will be:

MEDIUM

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

Two moles of an ideal gas, with

\frac{C_{P}}{C_{V}} = \frac{5}{3}

, are mixed with three moles of another ideal gas

\frac{C_{P}}{C_{V}} = \frac{4}{3}

. The value of

\frac{C_{P}}{C_{V}}

for the mixture is

HARD

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

$1$ mole of gas with $γ = \frac{7}{5}$ is mixed with $1$ mole of gas with $γ = \frac{5}{3}$ , then the value of $γ$ for the resulting mixture is

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

For a rigid diatomic molecule, the universal gas constant

R = n C_{P}

, where,

C_{P}

is the molar specific heat at constant pressure and

n

is a number. Hence,

n

is equal to

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

For a gas if

γ = 1.4,

then atomicity, specific heat capacity at constant pressure and specific heat capacity at constant volume of the gas are respectively

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

For a gas

C_{P} - C_{V} = R

in a state

P

and

C_{P} - C_{V} = 1.10 R

in a state

Q, T_{P}

and

T_{Q}

are the temperatures in two different states

P

and

Q

, respectively. Then

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

A monoatomic gas performs a work of $\frac{Q}{4}$ , where $Q$ is the heat supplied to it. The molar heat capacity of the gas will be _____ $R$ during this transformation, where $R$ is the gas constant.

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

The molar specific heat of an ideal gas at constant pressure and constant volume is

C_{p}

and

C_{υ}

respectively. If

R

is the universal gas constant and the ratio of

C_{p}

C_{υ}

γ

then

C_{υ} =

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

Let

γ_{1}

be the ratio of molar specific heat at constant pressure and molar specific heat at constant volume of a monoatomic gas and

γ_{2}

be the similar ratio of diatomic gas. Considering the diatomic gas molecule as a rigid rotator, the ratio

\frac{γ_{1}}{γ_{2}}

is:

MEDIUM

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

Consider two ideal diatomic gases

A

and

B

at some temperature

T

. Molecules of the gas

A

are rigid, and have a mass

m

. Molecules of the gas

B

have an additional vibrational mode and have a mass

\frac{m}{4}

. The ratio of the specific heats

{(C_{V}^{})}_{A} and {(C_{V}^{})}_{B}

of gas

A

and

B,

respectively is:

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

An ideal gas has molecules with

5

degrees of freedom. The ratio of specific heats at constant pressure

(C_{p})

and at constant volume

(C_{V})

is:

EASY

Physics>Heat and Thermodynamics>Molecular Properties of Matter>Specific Heat of Gas

C_{p} - C_{v} = \frac{R}{M}

and

C_{v}

are specific heats at constant pressure and constant volume respectively. It is observed that,

C_{p} - C_{v} = a

for hydrogen gas and

C_{p} - C_{v} = b

for nitrogen gas. The correct relation between

a

and

b

is:

Derive the formula for the molar specific heat capacity at constant volume of a mixture of two gases.

Important Questions on Molecular Properties of Matter

Learn and Prepare for any exam you want !