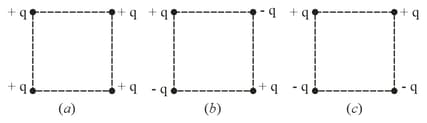
Determine the interaction energy of the point charges located at the corners of a square with the side $a$, in the circuits shown in the figures.

There is an infinite straight chain of alternating charges $q$ and $-q$. The distance between the neighbouring charges is equal to $a$. Find the interaction energy of each charge with all the others. Instruction: Make use of the expansion of $\ln (1+\alpha )$ in a power series in $\alpha$.

A point charge $q$ is located at a distance $l$ from an infinite conducting plane. Find the interaction energy of that charge with those induced on the plane.

Calculate the interaction energy of two balls, whose charges $q_1$and $q_2$ are spherically symmetrical. The distance between the centres of the balls is equal to $l$.

Instruction: Start with finding the interaction energy of a ball and a thin spherical layer.

What amount of heat will be generated in the circuit shown, after the switch $Sw$ is shifted from position $1$ to position $2$?

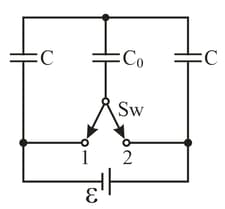
What amount of heat will be generated in the circuit shown in the figure, after the switch $Sw$ is shifted from position $1$ to position $2$?

A system consists of two thin concentric metal shells of radii $R_1$ and $R_2$ with corresponding charges $q_1$ and $q_2.$ Find the self energy values ${\left(U_{\mathrm{self}}\right)}_1$ and ${\left(U_{\mathrm{self}}\right)}_2$ of each shell, the interaction energy of the shells $U_{12}$, and the total electric energy of the system $U$.