Diameter is half of the radius.
Important Questions on Basic Geometrical Ideas
A sector of radius and central angle is rolled up into a cone. What is the central angle of the sector to be used to make a cone of base radius and height ?
The length of two chords and of a circle of centre are equal and then, is
Only one circle can be drawn through three non collinear points.
In the given figure, is the diameter of a circle and then is equal to
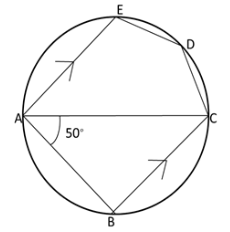
In the given figure, is a pentagon inscribed in a circle such that is a diameter and side . If , find giving reason .
In the figure, the chord is perpendicular to the diameter . Find the measure of . (in ).
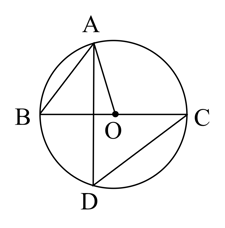
is the diameter of the circle. is the point on the circle.
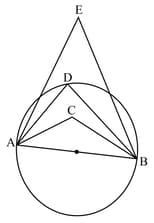
. The measure of one among and is . Write the measures of .
Prove that, the angle in the semicircle is right angle.
The angle subtended by the diameter of a circle at a point on the circumference is _____.
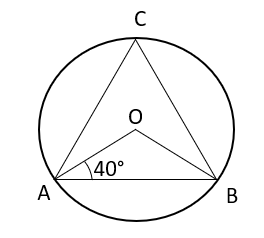
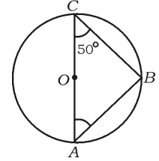
In the given figure is centre of a circle, and then the value of will be
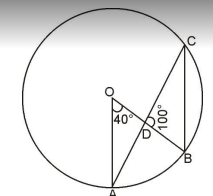
On the circle with center , points are such that . A point is located on the tangent at to the circle such that and are on the opposite sides of the line and . The line segment intersects the circle again at . Then the ratio is equal to -
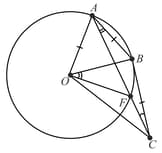
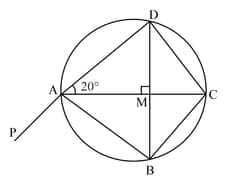
In the figure, is the centre of a circle, is a diameter. If , then find the measure of (in ).
To construct two tangents from a point 'P' outside the circle.
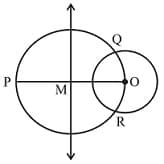
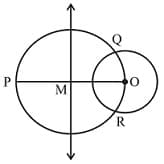
PQ is
Give a geometrical construction for finding the fourth point lying on a circle passing through three given points, without finding the center of the circle. Justify the construction.