MEDIUM

IOQM - PRMO and RMO

IMPORTANT

Earn 100

Different positive $3$ -digit integers are formed from the five digits $1, 2, 3, 5, 7,$ and repetitions of the digits are allowed. As an example, such positive $3$ -digit integers include $352, 577, 111,$ etc. Now, the sum of all the distinct positive $3$ -digit integers formed in this way is written as $A B C 50$ . Find $A + B + C$ .

50% studentsanswered this correctly

Important Questions on Counting

EASY

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-1 for PRMO>Chapter 3 - Counting>EXERCISE>Q 9

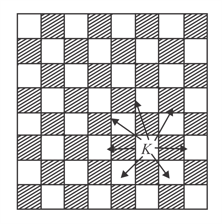
As shown in the picture, the knight can move to any of the indicated squares of the $8 \times 8$ chessboard in $1$ move. If the knight starts from the position shown, find the number of possible landing positions after $20$ consecutive moves.

Question Image

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-1 for PRMO>Chapter 3 - Counting>EXERCISE>Q 10

There are

N

number of

11

-digit positive integers such that the digits from left to right are non-decreasing. (For example,

(12345678999, 55555555555, 23345557889) .

Find the sum of all the digits of

N

MEDIUM

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-1 for PRMO>Chapter 3 - Counting>EXERCISE>Q 11

A four digit number consists of two distinct pairs of repeated digits (for example

2211, 2626

and

7007

) .

Find the total number of such possible numbers that are divisible by

7

101

but not both.

MEDIUM

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-1 for PRMO>Chapter 3 - Counting>EXERCISE>Q 12

m

and

n

are two positive integers satisfying

1 \leq m \leq n \leq 40 .

Find the number of pairs of

(m, n)

such that their product

m n

is divisible by

33

EASY

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-1 for PRMO>Chapter 3 - Counting>EXERCISE>Q 13

How many

7

digit palindromes (numbers that read the same backward as forward) can be formed using the digits

2, 2, 3, 3, 5, 5, 5

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-1 for PRMO>Chapter 3 - Counting>EXERCISE>Q 14

Ajay refuses to sit next to either Bharat or Chandan. Deepak refuses to sit next to Enees. How many ways are there for the five of them to sit in a row of

5

chairs under these conditions?

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-1 for PRMO>Chapter 3 - Counting>EXERCISE>Q 15

If there are

N

integers between

100

and

999

, inclusive, have the property that some permutation of its digits is a multiple of

11

between

100

and

999 ?

For example, both

121

and

231

have this property. Then find the value of

\frac{N - 1}{5} .

HARD

IOQM - PRMO and RMO

IMPORTANT

Non-Routine Mathematics Resource Book-1 for PRMO>Chapter 3 - Counting>EXERCISE>Q 16

The numbers

1, 2, 3, 4, 5

are to be arranged in a circle. An arrangement is bad if it is not true that for every

n

from

1

15

one can find a subset of the numbers that appear consecutively on the circle that sum to

n .

Arrangements that differ only by a rotation or a reflection are considered the same. How many different bad arrangements are there?

Important Questions on Counting

Learn and Prepare for any exam you want !