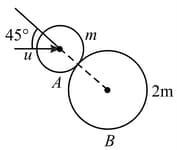
Disc $A$ of mass $m$ collides with stationary disc $B$ of mass $2m$ as shown in figure. Find the value of coefficient of restitution for which the two discs move in perpendicular direction after collision.

A mass ${\mathrm{m}}_1$ with initial speed $v_0$ in the positive $x$ -direction collides with a mass ${\mathrm{m}}_2=2{\mathrm{m}}_1$ which is initially at rest at the origin, as shown in figure. After the collision ${\mathrm{m}}_1$ moves off with speed ${\mathrm{v}}_1=\frac{{\mathrm{v}}_{\circ }}{2}$ in the negative $y$ -direction, and ${\mathrm{m}}_2$ moves off with speed $v_2$ at angle $\theta .$

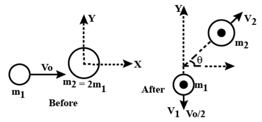
(a) Find the velocity (magnitude and direction) of the centre of mass before the collision, as well as its velocity after the collision.
(b) Find ${\mathrm{v}}_2$ in terms of ${\mathrm{v}}_{\circ }.$

A smooth ball ' $A$ 'travels towards another identical ball ' $B$ with a velocity $u.$ Ball $B$ is at rest and the impact parameter $d$ is equal to $\sqrt{3}R$ where $R$ is radius of each ball. Due to impact the direction of motion of ball $A$ changes by $30°.$ Find the velocities of the balls ' $A$ ' and ' $B$ 'after collision. It is given that collision is elastic.

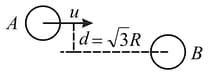
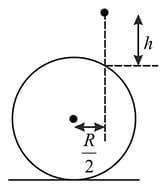
A small particle of mass $\mathrm{m}$ is released from a height $h$ on a large smooth sphere kept on a perfectly smooth surface, as shown in the figure. Collision between particle and sphere is perfectly inelastic. Determine the velocities of particle and sphere after collision.

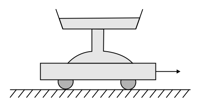
Sand is falling on a flat car being pulled with constant speed. The rate of mass falling on the cart is constant. Then the horizontal component of force exerted by the falling sand on the cart,

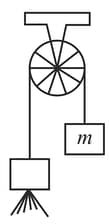
A mass ${\mathrm{m}}_1$is connected by a weightless cable passing over a frictionless pulley to a container of water, whose mass is ${\mathrm{m}}_0$ at $t=0.$ If the container ejects water in downward direction at a constant rate $b \mathrm{kg} s^{-1}.$ With a velocity $v_0$ relative to the container, determine the acceleration of ${\mathrm{m}}_1$ as a function of time.

A uniform chain of mass $\mathrm{m} = 1\mathrm{kg}$ and length $l = 1\mathrm{m}$ hangs on a thread and touches the surface of a table by its lower end. Find the force exerted by the table on the chain when $\mathrm{x} = 0.5 \mathrm{m}$ length of chain has fallen on the table. The fallen part does not form heap.

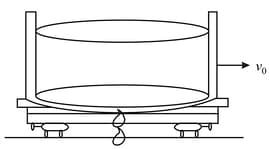
A smooth container filled with water moves with a velocity $v_0.$ If water leaks at the base with a constant rate $\mu \mathrm{kg}/\mathrm{s},$ find the velocity and acceleration of the container as the function of time. Assume $M=$ initial mass of the system (container $+$ water).