MEDIUM
Earn 100
Does Euclid fifth postulate imply the existence of parallel lines? Explain.
Important Questions on Introduction to Euclid's Geometry
MEDIUM
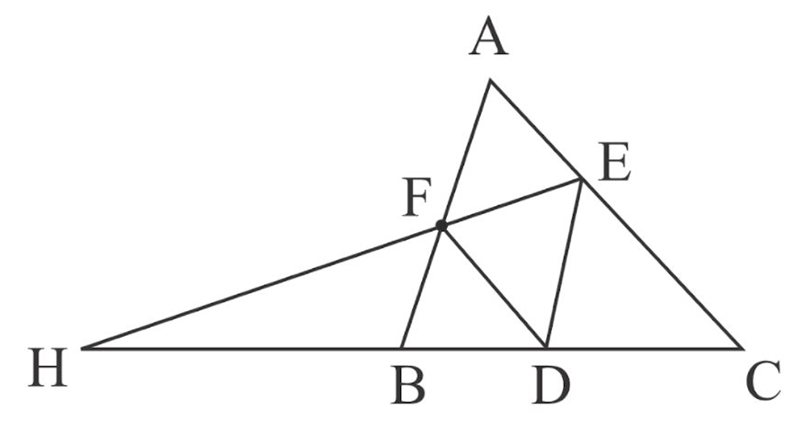
Given : is any point on side of . and . and meet at when produced as shown in the fig. Prove that:
EASY
is a trapezium in which and its diagonals intersect each other at point . Show that,
EASY
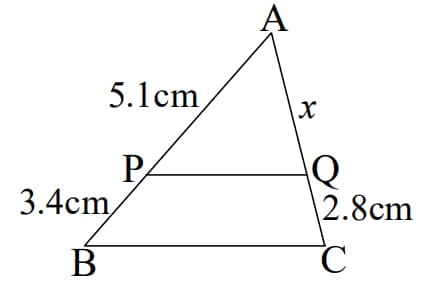
In the adjoining figure, if , Find .
MEDIUM
In the figure, and . If , find .
MEDIUM
is a trapezium in which and its diagonal intersect each other at a point . Show that:
MEDIUM
is trapezium in which and its diagonals intersect each other at the point . Prove that .
EASY
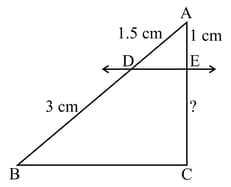
In the given figure, . Find
HARD
If a line is drawn parallel to one side of a triangle to intersects the other two sides in distinct points, the other two sides are divided in the same ratio. Prove it.
MEDIUM
State and prove Basic Proportionality theorem.
MEDIUM
State and prove Basic Proportionality Theorem.
MEDIUM
Prove that if we draw a line which is parallel to any one side of a triangle and intersects the other two sides at different points, then this line divides these two sides in the same ratio.
MEDIUM
Given : In where the points and lie on and respectively, and
Prove that :
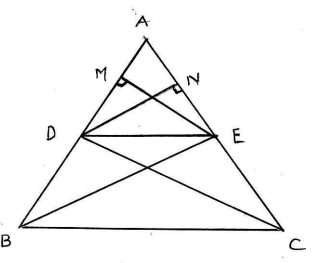
HARD
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. Prove it.
MEDIUM
If each exterior angle of a regular polygon is , find the number of sides of the polygon.
MEDIUM
The line parallel to of meets and at and respectively. If , and , then find the length of .
EASY
In . If and , then _____.
HARD
Let be an acute-angled triangle and let be its orthocentre. Let and be the centroids of the triangles and respectively. If the area of triangle is units, what is the area of triangle ?
EASY
A solid has _______.
HARD
Point is called a mid-point of line segment , prove that every line segment has one and only one mid-point.

