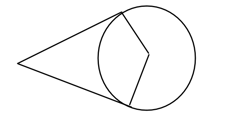
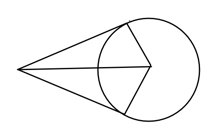
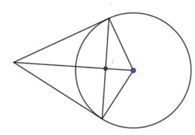
Draw a circle of radius $2.5$ centimetres. Draw a triangle of angles $40°, 80°, 60°$ with all its sides touching the circle.

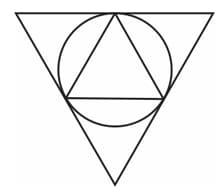
In the picture, the small triangle is equilateral. The sides of the large triangle are tangents to the circumcircle of the small triangle at its vertices.
Prove that the large triangle is also equilateral and its sides are double those of the small triangle.

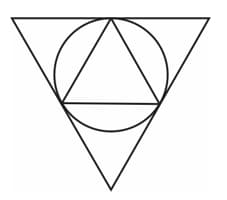
In the picture, the small triangle is equilateral. The sides of the large triangle are tangents to the circumcircle of the small triangle at its vertices.

Draw this picture, with sides of the smaller triangle $3$ centimetres.

The picture shows the tangents at two points on a circle and the radii through the points of contact.

Prove that the tangents have equal length.

The picture shows the tangents at two points on a circle and the radii through the points of contact.

Prove that the line joining the centre and the point where the tangents meet bisects the angle between the radii.

The picture shows the tangents at two points on a circle and the radii through the points of contact.

Prove that the line joining the centre and the point where the tangents meet is the perpendicular bisector of the chord joining the points of contact.

Prove that the quadrilateral with sides as the tangents at the ends of a pair of perpendicular chords of a circle is cyclic.

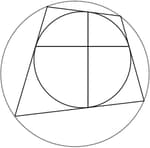
What sort of quadrilateral do we get if one chord is a diameter?

In the picture, the sides of the large triangle are tangents to the circumcircle of the small triangle, through its vertices.

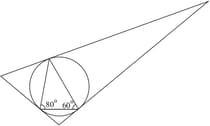
Calculate the angles of the large triangle.

In the picture, the sides of the large triangle are tangents of the circumcircle of the smaller triangle, through its vertices.

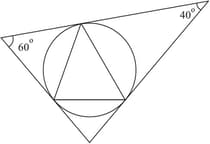
Calculate the angles of the smaller triangle.