MEDIUM
Earn 100
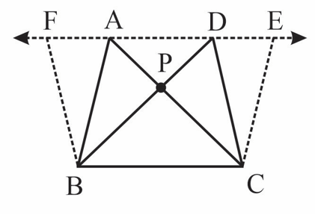
Draw two triangles and on the same base and between the same parallels as shown in the figure with as the point of intersection of and . Draw and such that and lie on line .
Can you show

Important Questions on Area of Parallelogram and Triangles
EASY
In and .The true relation among the following:
EASY
A triangular corner is cut from a rectangular piece of paper and the resulting pentagon has sides in some order. The ratio of the area of the pentagon to the area of the rectangle is-
HARD
Prove that, if a line is drawn parallel to one side of a triangle intersecting the other two sides, then the other two sides are divided in the same ratio.
MEDIUM
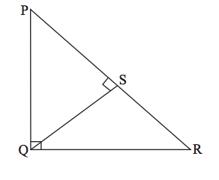
and are the altitudes of . If , then ___
MEDIUM
In is the median and is a point on such that . Then area area is equal to:
MEDIUM
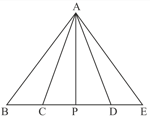
In the figure, and is mid-point of . The area of is
EASY
If the bases of two triangles are situated on the same line and the other vertex of the two triangles are common, then the ratio of the areas of two triangles are _____ to the ratio of their bases.
MEDIUM
A circle is inscribed in a right-angled triangle of perimeter . Then the ratio of numerical values of circumference of the circle to the area of the right-angled triangle is
EASY
Triangle PDC is drawn inside the square ABCD of side where P lies on AB. What is the area of the triangle?
EASY
The base and hypotenuse of a right-angled triangle are respectively. What is the area of the reiangle?
MEDIUM
What is the area of the triangle having sides and ?
HARD
What will be the area of triangle whose vertices are and ?
EASY
What is the area (in ) of an equilateral triangle whose side is ?
HARD
Prove that if a line is drawn parallel to one side of triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
EASY
Let be a triangle in which and Given below are the steps of constructing the Which of the following steps is INCORRECT?
Step I: Draw a line segment of length
Step II: Draw an at point of line segment
Step III: Cut off on the ray
Step IV: Join .
Step V: Draw bisector of which intersect ray at Join
Step VI: is the required triangle.
MEDIUM
Construct , in which and .
EASY
Which of the following options is INCORRECT?
HARD
Construct a in which and .
MEDIUM
Construct , such that , .
MEDIUM
Construct , in which , and

