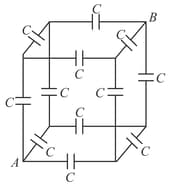
Each edge of the cube contains a capacitance $C$. The equivalent capacitance between the points $A$ and $B$ will be 

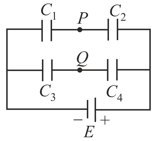
The potential difference between the points $P$ and $Q$ in the adjoining circuit will be

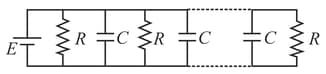
$n$ resistances each of resistance $R$ are joined with capacitors of capacity $C$ (each) and a battery of emf $E$ as shown in the figure. In steady state condition, ratio of charge stored in the first and last capacitor is:

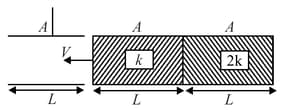
A parallel plate capacitor without any dielectric has capacitance $C_0$. A dielectric slab is made up of two dielectric slabs of dielectric constants $k$ and $2k$ and is of same dimensions as that of capacitor plates and both the parts are of equal dimensions arranged serially as shown. If this dielectric slab is introduced (dielectric $k$ enters first) in between the plates at a constant speed $V$, then a variation of capacitance with time will be best represented by:

An isolated metallic object is charged in vacuum to a potential $V_0$ using a suitable source, its electrostatic energy being $W_0$. It is then disconnected from the source and immersed in a large volume of dielectric with dielectric constant $K$. The electrostatic energy of the sphere in the dielectric is:

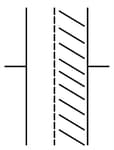
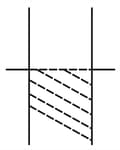
Consider a parallel plate capacitor. When half of the space between the plates is filled with some dielectric material of dielectric constant K as shown in $\mathrm{Figure} \left(1\right)$ below, the capacitance is $C_1$. However, if the same dielectric material fills half the space as shown in $\mathrm{Figure} \left(2\right)$, the capacitance is $C_2$. Therefore, the ratio $C_1:C_2$ is 

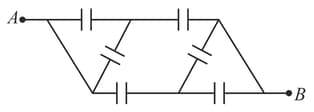
A network of six identical capacitors, each of capacitance $C$ is formed as shown below. The equivalent capacitance between the point$A$ and $B$ is

A capacitor of capacitance $2.0 \mathrm{\mu F}$ is charged to a potential difference of $12 \mathrm{V}$. It is then connected to an uncharged capacitor of capacitance$4.0 \mathrm{\mu F}.$

Find:

$\left(\mathrm{a}\right)$ The charge flow through connecting wire till steady-state on each of the two capacitors after the connection in $\mathrm{\mu C}$.

$\left(\mathrm{b}\right)$ The total electrostatic energy stored in both capacitors in $\mathrm{\mu J}$.

$\left(\mathrm{c}\right)$ The heat produced during the charge transfer from one capacitor to the other in $\mathrm{\mu J}.$