HARD
12th Karnataka Board
IMPORTANT
Earn 100
Explain how crossed and fields serve as a velocity selector.

Important Questions on Moving Charges and Magnetism
HARD
12th Karnataka Board
IMPORTANT
The frequency of cyclotron is 107 Hz. What should be operating magnetic field for accelerating protons ? If the radius of the dee’s of the cyclotrons is 6 x 10-1 m, calculate the energy of the proton beam produced by it in MeV. Given e = 1.6 x 10-19 C, Mp = 1.67 x 10-27 kg. 1 MeV = 1.602 x 10-13 J.
EASY
12th Karnataka Board
IMPORTANT
Why cyclotron is not used to accelerate light charged particles?
HARD
12th Karnataka Board
IMPORTANT
A current is flowing through a thin, straight metallic conductor of infinite length. Find expression for the magnetic field at a distance from it.
HARD
12th Karnataka Board
IMPORTANT
What do you mean by Biot-Savart’s law? Derive expression for magnetic field due a current-carrying conductor of infinite length. Name the rule which determines the direction of the magnetic field.
HARD
12th Karnataka Board
IMPORTANT
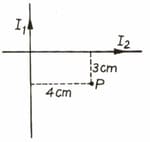
Two infinitely long insulated wires are kept perpendicular to each other. They carry currents and .
(i) Find the magnitude and direction of the magnetic field at .
HARD
12th Karnataka Board
IMPORTANT
Two parallel wires separated by carry currents of each in the opposite directions. Find the magnetic induction for the points between the wires at a distance from each wire.
HARD
12th Karnataka Board
IMPORTANT
Two concentric circular coils X and Y of radii and , respectively, lie in the same vertical plane containing the north to south direction. Coil X has turns and carries a current of ; coil Y has and carries a current of . The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
MEDIUM
12th Karnataka Board
IMPORTANT
For a circular coil of radius R and N turns carrying current I; the magnitude of the magnetic field at a point on its axis at a distance from its centre is given by,
Show that this reduces to the familiar result for the field at the centre of the coil.
