Figure  shows an aluminum rod joined to a copper rod. Each of the rods has a length of $20 \mathrm{cm}$ and area of cross-section $0·20 {\mathrm{cm}}^2$. The junction is maintained at a constant temperature $40 °\mathrm{C}$ and the two ends are maintained at $80 °\mathrm{C}$. Calculate the amount of heat taken out from the cold junction in one minute after the steady-state is reached. The conductivities are $K_{\mathrm{At}}=200 \mathrm{W} {\mathrm{m}}^{-1 }°{\mathrm{C}}^{-1}$ and $K_{\mathrm{Cu}}=400 \mathrm{W} {\mathrm{m}}^{-1 }°{\mathrm{C}}^{-1}$.

1. Heat Transfer:

There are three modes by which heat energy transfers from a body at a higher temperature to a body at a lower temperature.

(i) In conduction, heat is transferred from one point to another without the actual motion of heated particles.

(ii) In the process of convection, the heated particles of matter actually move.

(iii) In radiation, the intervening medium is not affected and heat is transferred without any material medium.

2. Thermal conduction:

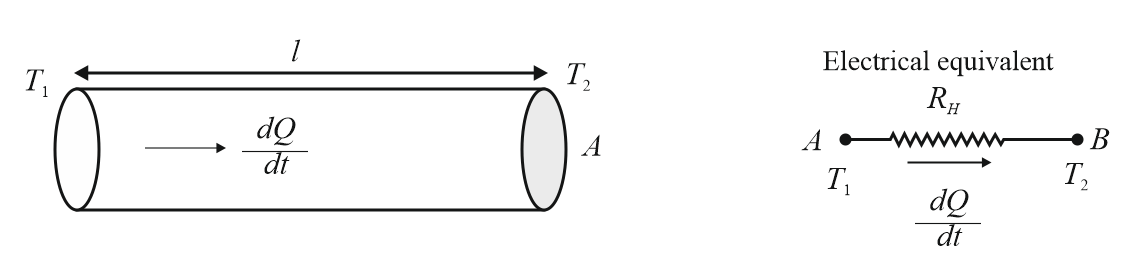
(i) Variable state: In this state temperature of each part of the rod increases.

(ii) Steady state: At this stage temperature of each part of the rod becomes constant.

(iii) Temperature gradient: Rate of change of temperature with the distance between any two points along the length of the rod.

Temperature gradient $=\frac{-\mathrm{\Delta }T}{\mathrm{\Delta }x}$

Unit: $\mathrm{K}/\mathrm{m} \mathrm{or} °\mathrm{C}/\mathrm{m}$

(iv) Rate of heat flow(in steady state) $\frac{\mathrm{d}Q}{\mathrm{d}t}=-KA\frac{\mathrm{d}T}{\mathrm{d}x}$ or $\frac{Q}{t}=\frac{KA\left(T_1-T_2\right)}{l}$

(v) Thermal resistance $R_{\mathrm{H}}=\frac{l}{KA}$

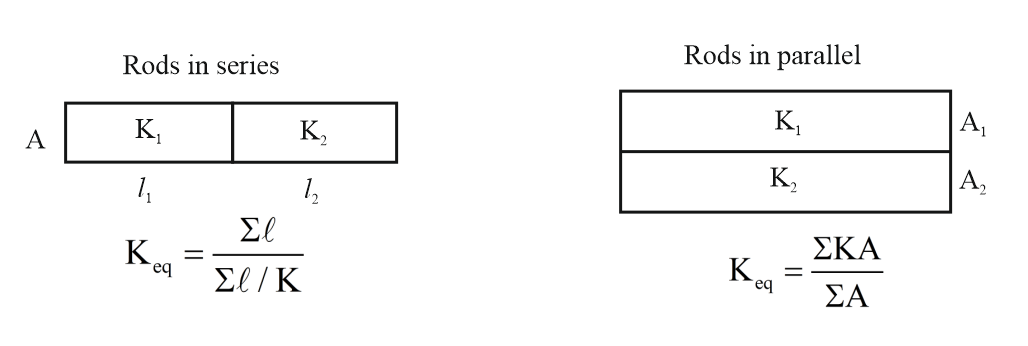
(vi) Growth of Ice on Ponds

Time taken by ice to grow a thickness from x1 to $x_2: t=\frac{\rho L}{2 K\theta }\left(X_2^2-X_1^2\right)$

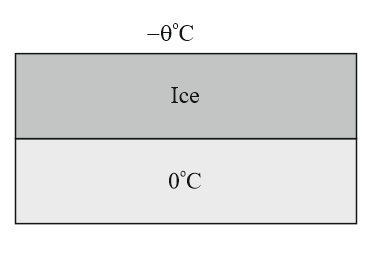
[K= thermal conductivity of ice, ρ= density of ice ]

3. Radiation:

Energy transfer in the form of electromagnetic waves through any medium.

Due to incident radiations on the surface of a body following phenomena occur by which the radiation is divided into three parts.

(i) Reflection

(ii) Absorption

(iii) Transmission

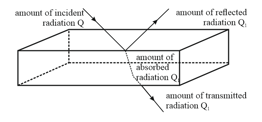
From energy conservation

(a) $Q=Q_{\mathrm{r}}+Q_{\mathrm{a}}+Q_{\mathrm{t}}\Rightarrow \frac{Q_{\mathrm{r}}}{Q}+\frac{Q_{\mathrm{a}}}{Q}+\frac{Q_{\mathrm{t}}}{Q}=1\Rightarrow r+a+t=1$

(b) Reflective Coefficient: $r=\frac{Q_{\mathrm{r}}}{Q}$

(c) Absorptive Coefficient: $a=\frac{Q_{\mathrm{a}}}{Q}$

(d) Transmittive Coefficient: $t=\frac{Q_{\mathrm{t}}}{Q}$

(e) r=1 and a=0, t=0 ⇒ Perfect reflector

(f) a=1 and r=0, t=0 ⇒ Ideal absorber (ideal black body)

(g) t=1 and a=0, r=0 ⇒ Perfect transmitter (Daithermanons)

(h) Reflection power $\left(r\right)=\left[\frac{Q_{\mathrm{r}}}{Q}\times 100\right]\mathrm{\%}$

(i) Absorption power $\left(a\right)=\left[\frac{Q_{\mathrm{a}}}{Q}\times 100\right]\mathrm{\%}$

(j) Transmission power $\left(t\right)=\left[\frac{Q_{\mathrm{t}}}{Q}\times 100\right]\mathrm{\%}$

(k) A hot body emits radiation of all wavelengths.

(l) The wavelength corresponding to maximum emission of radiations shifts from longer wavelength to shorter wavelength as the temperature increases. Due to this, the color of a body appears to be changing.

4. Prevost's theory of heat exchange: A body is simultaneously emitting radiations to its surroundings and absorbing radiations from the surroundings.

5. Stefan's Boltzmann law:

Radiated energy emitted by a perfect black body per unit area/sec is $E=\sigma T^4$

(i) For a general body $E=\sigma e_{\mathrm{r}}{T}^4$[Where $0 \le e_{\mathrm{t}} \le 1$]

(ii) If surrounding has temperature T0, then $E_{\mathrm{nel}}=e_{\mathrm{r}}\sigma \left(T^4-T_0^4\right)$

6. Newton's law of cooling:

If temperature difference is small

Rate of cooling $\frac{\mathrm{d}\theta }{\mathrm{d}t}\propto \left(\theta -{\theta }_0\right)$

$\Rightarrow \theta ={\theta }_0+\left({\theta }_1-{\theta }_0\right)e^{-kt}$

[where k= constant]

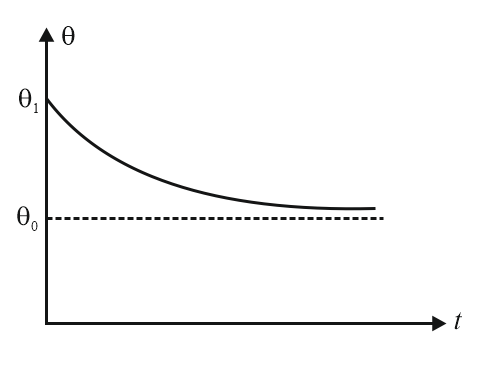
when a body cools from θ1 to θ2 in time '$t$' in a surrounding of temperature θ0 then, θ1-θ2t=kθ1+θ22-θ0 [where k=constant]

7. Kirchhoff's law:

The ratio of emissive power to absorptive power is same for all surfaces at the same temperature and is equal to the emissive power of a perfectly black body at that temperature. ea=EA=E1⇒ea=E ⇒ e ∝ a

Therefore, a good absorber is a good emitter.

(i) Perfectly Black Body: A body that absorbs all the radiation incident on it is called a perfectly black body.

(ii) Absorptive Power (a): Absorptive power of a surface is defined as the ratio of the radiant energy absorbed by it in a given time to the total radiant energy incident on it in the same time.

For an ideal black body, absorptive power =1

(iii) Emissive power (e): For a given surface it is defined as the radiant energy emitted per second per unit area of the surface.

8. Wien's Displacement Law:

Product of the wavelength ${\lambda }_{\mathrm{m}}$ of most intense radiation emitted by a black body and absolute temperature of the black body is a constant ${\lambda }_{\mathrm{m}} T=b=2.89\times {10}^{-3} \mathrm{mK}=$ Wein's constant

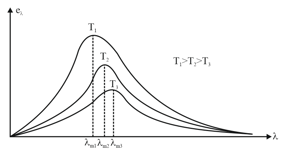
Area under $e_{\mathrm{\lambda }}-\lambda$ graph $={\int }_0^{\infty }{e}_{\mathrm{\lambda }}d\lambda =e=\sigma T^4$

9. Solar Constant:

The energy emitted by the sun per sec (Where $R$ is the radius of the sun and $T$ its temperature),

This energy will spread over a sphere of radius $r$ ($=$ average distance between sun and earth); while reaching Earth so the intensity of solar radiation at the surface of the earth (called solar constant $S$) will be given by

$S=\frac{P}{4\pi r^2}=\frac{4\pi R^2\sigma T^4}{4\pi r^2}=5.67\times 10^{-8}\frac{\mathrm{W}}{{\mathrm{m}}^2 {\mathrm{K}}^4}$