Figure shows a case in which the momentum component of a particle is fixed, so that, then, from Heisenberg's uncertainty principle, the position of the particle is completely unknown. From the same principle, it follows that the opposite is also true, that is, if the position of a particle is exactly known the uncertainty in its momentum is infinite.
Consider an intermediate case. In which the position of a particle is measured, not to infinite precision, but to within a distance of where is the particle's de Broglie wavelength. Show that the uncertainty in the (simultaneously measured) momentum component is then equal to the component itself; that is, Under these circumstances, would a measured momentum of zero surprises you? What about a measured momentum of Of Of
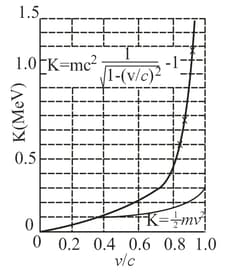


Important Questions on Photons and Matter Waves
The function displayed in Eq. can describe a free particle for which the potential energy is in Schrodinger's equation (Eq. ). Assume now that a constant in that equation. Show that Eq. is a solution of Schrodinger's equation with
giving the angular wave number of the particle.
The sun is approximately an ideal blackbody radiator with a surface temperature of Find the wavelength at which its spectral radiancy is maximum and identify the type of electromagnetic wave corresponding to that wavelength. (See Figure) The universe is approximately an ideal blackbody radiator with radiation emitted when atoms first formed. Today the spectral radiancy of that radiation peaks at a wavelength of (in the microwave region). What is the corresponding temperature of the universe?