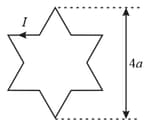
Find out magnetic field at point $O$ for the following current distributions.

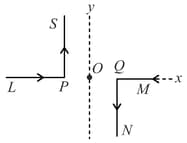
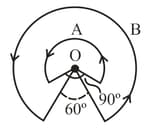
Two very long, straight, and insulated wires are kept at $90°$ angle from each other in $\mathrm{x}\mathrm{y}$ plane as shown in the figure.

These wires carry currents of equal magnitude $I$ , whose direction are shown in the figure. The net magnetic field at point $P$ will be:

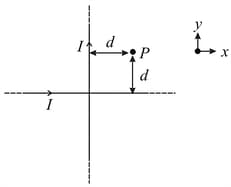
Find the magnetic field at point $\mathrm{P}$ due to a straight line segment $\mathrm{A}\mathrm{B}$ of length $6 \mathrm{c}\mathrm{m}$ carrying a current of $5 \mathrm{A}.$ (See figure) $\left({\mu }_0=4\pi \times {10}^{-7} {\mathrm{NA}}^{-2}\right)$

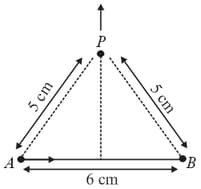
The magnetic field at the centre ${}^{\text{'}}O^{\text{'}}$ in the given figure is

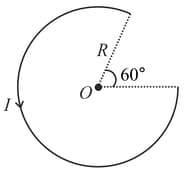
A wire $A$, bent in the shape of an arc of a circle, carrying a current of $2 \mathrm{A}$ and having radius $2 \mathrm{cm}$ and another wire $B$, also bent in the shape of an arc of a circle, carrying a current of $3 \mathrm{A}$ and having radius of $4\text{ cm}$, are placed as shown in the figure. The ratio of the magnetic fields due to the wires $\text{A}$ and $\text{B}$ at the common centre $\text{O}$ is:

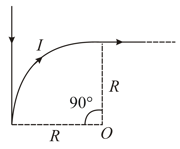
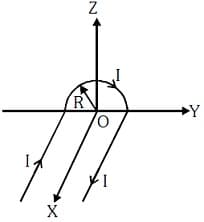
A wire carrying current $\text{I}$ has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to $\text{X}$ -axis while semicircular portion of radius $\text{R}$ is lying in $\text{Y}$ -$\text{Z}$ plane. Magnetic field at point $\text{O}$ is :

As shown in the figure, two infinitely long, identical wires are bent by ${90}^o$ and placed in such a way that the segments $LP$ and $QM$ are along the $x$ - axis, while segments $PS$ and $QN$ are parallel to the $y$ - axis. If $OP=OQ=4cm,$ and the magnitude of the magnetic field at $O$ is ${10}^{-4} T,$ and the two wires carry equal currents (see figure), the magnitude of the current in each wire and the direction of the magnetic field at $O$ will be $\left({\mu }_0=4\pi \times {10}^{-7}N{A}^{-2}\right):$