EASY
CAT
IMPORTANT
Earn 100

Find the angle AHC in the regular dodecagon shown below.

Question Image

50% studentsanswered this correctly

Important Questions on Geometry

EASY
CAT
IMPORTANT
Quantum CAT Also Useful for XAT>Chapter 12 - SNAP>CMAT>Q 129

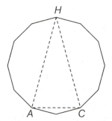
In the following figure the three equispaced vertices of a regular dodecagon are connected in such a way that they create a triangle, as shown below. If each side of the triangle is 32+3 cm, find the circumradius of the dodecagon.

Question Image

EASY
CAT
IMPORTANT
Quantum CAT Also Useful for XAT>Chapter 12 - SNAP>CMAT>Q 130

In the following figure the four equispaced vertices of a regular dodecagon are connected in such a way that they create a quadrilateral, as shown below. If each side of the quadrilateral is 3+1 cm, find the circumradius of the dodecagon.

Question Image

EASY
CAT
IMPORTANT
Quantum CAT Also Useful for XAT>Chapter 12 - SNAP>CMAT>Q 131
A regular dodecagon is inscribed in a circle of radius 1 cm. Find the area of the dodecagon
HARD
CAT
IMPORTANT
Quantum CAT Also Useful for XAT>Chapter 12 - SNAP>CMAT>Q 132
Circle with radii 3,4 and 5 touch each other externally, if P is the point of intersection of tangents to these circles at their points of contact. Find the distance of P from the point of contact.
EASY
CAT
IMPORTANT
Quantum CAT Also Useful for XAT>Chapter 12 - SNAP>CMAT>Q 133
Three points X, Y and Z are concyclic to the larger circle with radius 15 cm and there is another concentric circle with radius 8 cm such that XY and XZ are tangents to the smaller circle. At how many points does YZ intersect the larger circle?
EASY
CAT
IMPORTANT
Quantum CAT Also Useful for XAT>Chapter 12 - SNAP>CMAT>Q 136
Triangle ABC inscribes a circle with centre Oand inradius 6 cm. The inradius OD divides side BC at D, such that BD=2 cm and DC=8 cm. Find the ratio AB: AC.
EASY
CAT
IMPORTANT
Quantum CAT Also Useful for XAT>Chapter 12 - SNAP>CMAT>Q 137
A circle with radius 12 cm has two perpendicular chords AB and CD intersecting at a point R, other than the centre O, where RD=6 cm and RB=18 cm. Find the length of AR.
EASY
CAT
IMPORTANT
Quantum CAT Also Useful for XAT>Chapter 12 - SNAP>CMAT>Q 138
There are two tangents AT and BT on a circle of radius 30 cm. A line OT(=50 cm) connects the centre O with the external point T. Another tangent CD touches the circle at P such that C and D lie on the line segments AT and BT, respectively. Points P and T lie on the same side of the circle. Find the maximum possible area (in sq. cm ) of the circle inscribed in the triangle CDT.