The gap between the plates of a parallel-plate capacitor is filled with an isotropic dielectric, whose permittivity ε varies linearly from ε 1 to ε 2 ε 2 > ε 1 , in the direction perpendicular to the plates. The area of each plate equals S , the separation between the plates is equal to d . Find: (a) the capacitance of the capacitor; (b) the space density of the bound charges as a function of ε , if the charge of the capacitor is q and the field E → in it, is directed towards the growing ε values.

(a) Let us assume that the x -axis is directed towards the right, and place the origin on the left plate. Again, we assume that the left plate is positively charged. It is given in question that ε varies linearly. So, ε ( x ) = a + b x , where, the constants a and b can be determined from the given condition. It is given that ε = ε 1 , at x = 0 , and ε = ε 2 , at x = d . ε 1 = a + b × 0 ⇒ a = ε 1 ε 2 = ε 1 + b × d ⇒ b = ε 2 - ε 1 d Thus, ε x = ε 1 + ε 2 - ε 1 d x Now, the potential difference between the plates, φ + - φ - = ∫ 0 d E → · d r → = ∫ 0 d σ ε 0 ε ( x ) d x = ∫ 0 d σ ε 0 ε 1 + ε 2 - ε 1 d x d x = σ d ε 2 - ε 1 ε 0 ln ε 2 ε 1 Hence, the required value of capacitance, C = Q V = Q ∆ φ . Hence, C = σ S φ + - φ - = ε 2 - ε 1 ε 0 S ln ε 2 ε 1 d (b) Surface charge density on the left plate, σ = q S , and surface charge density of the bounded charge on dielectric, at a distance x from the left plate, P = q S - q S ε ( x ) . In this case, we get, x dependent surface charge density of the bounded charge. Hence, to get the space charge density, differentiating it with respect to x , so that the space density of bound charges ρ ' becomes, ρ ' = d P d x = d q S - q S ε x d x = 0 - q S × d 1 ε x d x = q S 1 ε 2 ( x ) d ε x d x ⇒ ρ ' = q ε 2 - ε 1 S ε 2 ( x ) d

HARD

JEE Main

IMPORTANT

Earn 100

Find the capacitance of an isolated ball-shaped conductor of radius $R_{1}$ , surrounded by an adjacent concentric layer of dielectric, with permittivity $ε$ and outside radius $R_{2}$ .

Important Questions on ELECTRODYNAMICS

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 3 - ELECTRODYNAMICS>ELECTRIC CAPACITANCE. ENERGY OF AN ELECTRIC FIELD>Q 3.102.

Two parallel-plate air capacitors, each of capacitance

C

, were connected in series to a battery with emf

ξ

. Then, one of the capacitors was filled up with uniform dielectric with permittivity

ε

. How many times did the electric field strength in that capacitor decrease? What amount of charge flows through the battery?

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 3 - ELECTRODYNAMICS>ELECTRIC CAPACITANCE. ENERGY OF AN ELECTRIC FIELD>Q 3.103.

The space between the plates of a parallel-plate capacitor is filled, consecutively, with two dielectric layers $1$ and $2$ , having thicknesses $d_{1}$ and $d_{2}$ and permittivities $ε_{1}$ and $ε_{2}$ , respectively. The area of each plate is equal to $S$ . Find:

(a) the capacitance of the capacitor;

(b) the density $σ'$ of the bound charges on the boundary plane, if the voltage across the capacitor equals $V$ , and the electric field is directed from layer $1$ to layer $2$ .

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 3 - ELECTRODYNAMICS>ELECTRIC CAPACITANCE. ENERGY OF AN ELECTRIC FIELD>Q 3.104.

The gap between the plates of a parallel-plate capacitor is filled with an isotropic dielectric, whose permittivity $ε$ varies linearly from $ε_{1}$ to $ε_{2} (ε_{2} > ε_{1})$ , in the direction perpendicular to the plates. The area of each plate equals $C$ , the separation between the plates is equal to $d$ . Find:

(a) the capacitance of the capacitor;

(b) the space density of the bound charges as a function of $ε$ , if the charge of the capacitor is $q$ and the field $\vec{E}$ in it, is directed towards the growing $ε$ values.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 3 - ELECTRODYNAMICS>ELECTRIC CAPACITANCE. ENERGY OF AN ELECTRIC FIELD>Q 3.105.

Find the capacitance of a spherical capacitor whose electrodes have radii $R_{1}$ and $R_{2} (R_{2} > R_{1})$ , and which is filled with isotropic dielectric whose permittivity varies as $ε = \frac{a}{r}$ , where $a$ is a constant and $r$ is the distance from the centre of the capacitor.

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 3 - ELECTRODYNAMICS>ELECTRIC CAPACITANCE. ENERGY OF AN ELECTRIC FIELD>Q 3.106.

A cylindrical capacitor is filled with two cylindrical layers of dielectric with permittivities

ε_{1}

and

ε_{2} .

The inside radii of the layers are equal to

R_{1}

and

R_{2} (R_{2} > R_{1})

. The maximum permissible values of electric field strength are equal to

E_{1 m}

and

E_{2 m}

, for these dielectrics. At what relationship between

ε_{1} R_{1}

and

E_{m}

, will the voltage increase result in the field strength reaching the breakdown value, for both dielectrics simultaneously?

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 3 - ELECTRODYNAMICS>ELECTRIC CAPACITANCE. ENERGY OF AN ELECTRIC FIELD>Q 3.107.

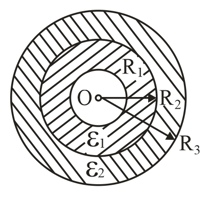
There is a double-layer cylindrical capacitor whose parameters are shown in the figure. The breakdown field strength values for these dielectrics are equal to $E_{1}$ and $E_{2}$ , respectively. What is the breakdown voltage of this capacitor, if $ε_{1} R_{1} E_{1} < ε_{2} R_{2} E_{2}$ ?

Question Image

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 3 - ELECTRODYNAMICS>ELECTRIC CAPACITANCE. ENERGY OF AN ELECTRIC FIELD>Q 3.108.

Two long straight wires with equal cross-sectional radii $a$ are located parallel to each other in air. The distance between their axes equals $b$ . Find the mutual capacitance of the wires per unit length, under the condition $b ≫ a$ .

HARD

JEE Main

IMPORTANT

Problems in General Physics>Chapter 3 - ELECTRODYNAMICS>ELECTRIC CAPACITANCE. ENERGY OF AN ELECTRIC FIELD>Q 3.110.

Find the capacitance of a system of two identical metal balls of radius

a

, if the distance between their centres is equal to

b

, with

b ≫ a

. The system is located in a uniform dielectric with permittivity

ε

Find the capacitance of an isolated ball-shaped conductor of radius R1, surrounded by an adjacent concentric layer of dielectric, with permittivity ε and outside radius R2.

Important Questions on ELECTRODYNAMICS

Learn and Prepare for any exam you want !

Find the capacitance of an isolated ball-shaped conductor of radius $R_{1}$ , surrounded by an adjacent concentric layer of dielectric, with permittivity $ε$ and outside radius $R_{2}$ .