EASY

Earn 100

Find the distance between the points $(- 5, 7)$ and $(- 1, 3)$ .

100% studentsanswered this correctly

Important Questions on Coordinate Geometry

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

The value of

p

, for which the points

A (3, 1)

B (5, p)

and

C (7, - 5)

are collinear is

MEDIUM

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

What is the area (in square units) of the triangular region enclosed by the graphs of the equations

x + y = 3, 2 x + 5 y = 12

and the

x

-axis?

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

P (8, 10)

and

Q (14, - 2)

are two given points and the point

R

divides the line-segment

P Q

externally in the ratio

8 : 6

. The coordinates of

R

are

HARD

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

The incentre of the triangle with vertices

(1, \sqrt{3}), (0, 0) and (2, 0)

is:

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

The equation of the graph shown here is:

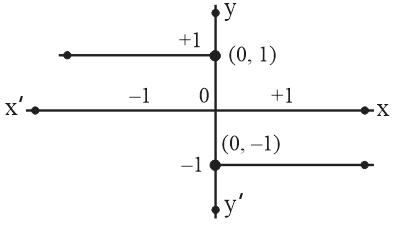
Question Image

HARD

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

If a circle of radius

R

passes through the origin

O

and intersects the coordinate axes at

A

and

B

, then the locus of the foot of perpendicular from

O

A B

is :

HARD

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

Let

S

be the focus of parabola

x^{2} + 8 y = 0

and

Q

be any point on it. If

P

divides the line segment

S Q

in the ratio

1 : 2,

then the locus of

P

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

Locus of the centre of rolling circle in a plane will be

HARD

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

If the distance between the points

(x, 0)

and

(- 7, 0)

10

. Then, the possible values of

x

are ______.

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

In the given figure, $A P$ bisect $∠ B A C$ . If $AB = 4 cm, AC = 6 cm$ and $BP = 3 cm$ , then the length of $CP$ is:

Question Image

MEDIUM

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

If the sum of distances from a point

P

on two mutually perpendicular straight lines is

1

unit, then the locus of

P

MEDIUM

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

Find the ratio in which line $3 x + 2 y = 17$ divides the line segment joined by points $(2, 5)$ and $(5, 2) .$

MEDIUM

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

Let

C

be the circle with centre

(0, 0)

and radius

3 unit

. The equation of the locus of the mid points of the chords of the circle

C

that subtend an angle of

\frac{2 π}{3}

at its centre, is:

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

Find the area of

∆ A B C

Whose vertices are

A (10, - 6), B (2, 5)

and

C (- 1, 3) .

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

A straight line through a fixed point

(2, 3)

intersects the coordinate axes at distinct points

P

and

Q

. If

O

is the origin and the rectangle

O P R Q

is completed, then the locus of

R

is:

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

A straight line through the origin

O

meets the parallel lines

4 x + 2 y = 9

and

2 x + y + 6 = 0

P

and

Q

respectively. The point

O

divides the segment

P Q

in the ratio

MEDIUM

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

P (- 3, - 2, 4), Q (- 9, - 8, 10)

and

R (- 5, - 4, 6)

are collinear, then the ratio in which

R

divides

P Q

EASY

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

△ ABC, D, E

and

F

are the midpoints of the sides AB, BC and CA, respectively. If

AB = 12 cm, BC = 20 cm

and

CA = 15 cm

, then the value of

\frac{1}{2} (DE + EF + DF)

is:

HARD

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

Find the area of the triangle formed by the lines

x - 3 y = 0, x - y = 4

and

x + y = 4 .

MEDIUM

Mathematics>Geometry>Coordinate Geometry>Coordinate System in 2D

Find the area of the triangle formed with the three straight lines represented by:

$(i) x + y = 0 (i i) 3 x = 5 y; a n d (i i i) y = 3 x - 12$

Find the distance between the points (-5,7) and (-1,3).

Important Questions on Coordinate Geometry

Learn and Prepare for any exam you want !

Find the distance between the points $(- 5, 7)$ and $(- 1, 3)$ .