The locus of the point of intersection of the lines 2 x - y + 4 2 k = 0 and 2 k x + k y - 4 2 = 0 ( k is any non-zero real parameter) is

a hyperbola with length of its transverse axis 8 2

an ellipse whose eccentricity is 1 3

a hyperbola whose eccentricity is 3

an ellipse with length of its major axis 8 2

MEDIUM

Earn 100

For $f (x) = m x,$ the area of the triangle formed by $(0, 0),$ the first quadrant point $P (a, f (a))$ and the reflection of that point $P$ about $y = x$ is $1000$ sq. units. If $m$ and $a$ are positive integers, then $m$ is

34.88% studentsanswered this correctly

Important Questions on Straight Lines

EASY

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

P (8, 10)

and

Q (14, - 2)

are two given points and the point

R

divides the line-segment

P Q

externally in the ratio

8 : 6

. The coordinates of

R

are

HARD

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

If a circle of radius

R

passes through the origin

O

and intersects the coordinate axes at

A

and

B

, then the locus of the foot of perpendicular from

O

A B

is :

HARD

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

If the distance between the points

(x, 0)

and

(- 7, 0)

10

. Then, the possible values of

x

are ______.

MEDIUM

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Let

S

be the set of all triangles in the

x y

-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in

S

has area

50

sq. units, then the number of elements in the set

S

is:

HARD

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Let

A (1, 0), B (6, 2)

and

C (\frac{3}{2}, 6)

be the vertices of a triangle

A B C .

P

is a point inside the triangle

A B C

such that the triangles

A P C, A P B

and

B P C

have equal areas, then the length of the line segment

P Q,

where

Q

is the point

(- \frac{7}{6}, - \frac{1}{3}),

MEDIUM

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

A point

P

moves on the line

2 x - 3 y + 4 = 0 .

Q (1, 4)

and

R (3, - 2)

are fixed points, then the locus of the centroid of

Δ P Q R

is a line:

MEDIUM

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Find the ratio in which line $3 x + 2 y = 17$ divides the line segment joined by points $(2, 5)$ and $(5, 2) .$

MEDIUM

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

The locus of the point of intersection of the lines

\sqrt{2} x - y + 4 \sqrt{2} k = 0

and

\sqrt{2} k x + k y - 4 \sqrt{2} = 0

(

k

is any non-zero real parameter) is

EASY

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Let

R = {(P, Q) | P

and

Q

are at the same distance from the origin

}

be a relation, then the equivalence class of

(1, - 1)

is the set

EASY

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Locus of the centre of rolling circle in a plane will be

HARD

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Let

B C

be a fixed line segment in the plane. The locus of a point

A

such that the triangle

A B C

is isosceles, is (with finitely many possible exceptional points)

MEDIUM

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Let

C

be the circle with centre

(0, 0)

and radius

3 unit

. The equation of the locus of the mid points of the chords of the circle

C

that subtend an angle of

\frac{2 π}{3}

at its centre, is:

MEDIUM

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Let

A = (a_{1}, a_{2})

and

B = (b_{1}, b_{2})

be two points in the plane with integer coordinates. Which one of the following is not a possible value of the distance between

A

and

B

MEDIUM

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

Locus of the image of the point $(2, 3)$ in the line $(2 x - 3 y + 4) + k (x - 2 y + 3) = 0, k \in R,$ is a

EASY

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

A B

is a straight line and

O

is point on the line

A B

. If one draws a line

O C

not coinciding with

O A

O B

, then the

∠ A O C

and

∠ B O C

are

HARD

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

A wall is inclined to the floor at an angle of $135 ° .$ A ladder of length $l$ is resting on the wall. As the ladder slides down, its mid-point traces an arc of an ellipse. Then the area of the ellipse is
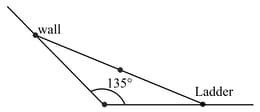
Question Image

HARD

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

In a circle with centre

O

, suppose

A, P, B

are three points on its circumference such that

P

is the mid-point of minor arc

A B

. Suppose when

∠ A O B = θ, \frac{a r e a (Δ A O B)}{a r e a (Δ A P B)} = \sqrt{5} + 2

∠ A O B

is doubled to

2 θ,

then the ratio

\frac{a r e a (Δ A O B)}{a r e a (Δ A P B)}

is.

HARD

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

The incentre of the triangle with vertices

(1, \sqrt{3}), (0, 0) and (2, 0)

is:

EASY

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

A straight line through a fixed point

(2, 3)

intersects the coordinate axes at distinct points

P

and

Q

. If

O

is the origin and the rectangle

O P R Q

is completed, then the locus of

R

is:

MEDIUM

Mathematics>Coordinate Geometry>Straight Lines>Basics of 2D Coordinate Geometry

If the sum of distances from a point

P

on two mutually perpendicular straight lines is

1

unit, then the locus of

P

For fx=mx, the area of the triangle formed by 0,0, the first quadrant point Pa,fa and the reflection of that point P about y=x is 1000 sq. units. If m and a are positive integers, then m is

Important Questions on Straight Lines

Learn and Prepare for any exam you want !

For $f (x) = m x,$ the area of the triangle formed by $(0, 0),$ the first quadrant point $P (a, f (a))$ and the reflection of that point $P$ about $y = x$ is $1000$ sq. units. If $m$ and $a$ are positive integers, then $m$ is