EASY
Agniveer Vayu
IMPORTANT
Earn 100

Four particles each of mass m are placed at the corners of a square of side length l. Then the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is

50% studentsanswered this correctly

Important Questions on Systems of Particles and Rotational Motion

MEDIUM
Agniveer Vayu
IMPORTANT
Achieve Indian Airforce Agniveer Vayu Physics Practice Book>Chapter 7 - Systems of Particles and Rotational Motion>Exercise>Q 4

Three point sized bodies each of mass M are fixed at three corners of light triangular frame of side length L. About an axis perpendicular to the plane of frame and passing through centre of frame the moment of inertia of three bodies is ML2.

In above problem about an axis passing through any side of frame the moment of inertia of three bodies is

MEDIUM
Agniveer Vayu
IMPORTANT
Achieve Indian Airforce Agniveer Vayu Physics Practice Book>Chapter 7 - Systems of Particles and Rotational Motion>Exercise>Q 5
Four spheres each of mass M and radius R are placed with their centers on the four corners A,B,C and D of a square of side b. The spheres A and B are hollow and C and D are solids. The moment of inertia of the system about side AD of square is
EASY
Agniveer Vayu
IMPORTANT
Achieve Indian Airforce Agniveer Vayu Physics Practice Book>Chapter 7 - Systems of Particles and Rotational Motion>Exercise>Q 6
Three point masses, each of mass m are placed at the corners of an equilateral triangle of side l. Moment of inertia of this system about an axis along one side of triangle is
EASY
Agniveer Vayu
IMPORTANT
Achieve Indian Airforce Agniveer Vayu Physics Practice Book>Chapter 7 - Systems of Particles and Rotational Motion>Exercise>Q 7
Moment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis ⊥ to its plane and passing through  a point on its  periphery  will be
EASY
Agniveer Vayu
IMPORTANT
Achieve Indian Airforce Agniveer Vayu Physics Practice Book>Chapter 7 - Systems of Particles and Rotational Motion>Exercise>Q 8
The diameter of a flywheel is increased by 1%. Increase in its moment of inertia about the central axis is
EASY
Agniveer Vayu
IMPORTANT
Achieve Indian Airforce Agniveer Vayu Physics Practice Book>Chapter 7 - Systems of Particles and Rotational Motion>Exercise>Q 9
Two discs have same mass and thickness. Their materials have densities d1 and d2. The ratio of their moments of inertia about central axis will be
EASY
Agniveer Vayu
IMPORTANT
Achieve Indian Airforce Agniveer Vayu Physics Practice Book>Chapter 7 - Systems of Particles and Rotational Motion>Exercise>Q 1
Figure shows a body of arbitrary shape 'O' is the centre of mass of the body and mass of the body is M. If ICC′=I0 then IAA′ will be equal to

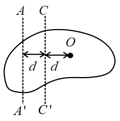
Question Image
MEDIUM
Agniveer Vayu
IMPORTANT
Achieve Indian Airforce Agniveer Vayu Physics Practice Book>Chapter 7 - Systems of Particles and Rotational Motion>Exercise>Q 2
The moment of inertia of a solid sphere of radius R about its diameter is same as the that of disc of radius 2R about its diameter. The ratio of their masses is -