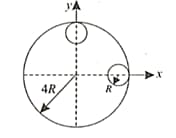
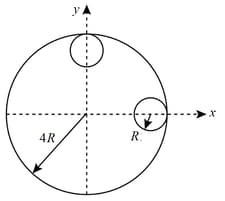
From the circular disc of radius $4R$, two small discs of radii$R$are cut-off. The center of mass of the new structure will be,

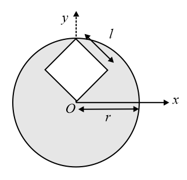
A disc (of radius $r \mathrm{cm}$) of uniform thickness and uniform density $\rho$ has a square hole with sides of length, $l=\frac{r}{\sqrt{2}} \mathrm{cm}$. One corner of the hole is located at the center of the disc and center of the hole lies on $y$-axis as shown. Then, the $y$-coordinate of position of center of mass of disc with hole (in $\mathrm{cm}$) is,

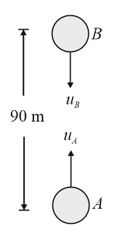
Two particles $A$ and $B$ of masses $1 \mathrm{kg}$ and $2 \mathrm{kg}$, respectively, are projected in the same vertical line as shown in the figure with speeds $u_{\mathrm{A}}=200 \mathrm{m} {\mathrm{s}}^{-1}$ and $u_{\mathrm{B}}=85 \mathrm{m} {\mathrm{s}}^{-1}$, respectively. Initially, they were $90 \mathrm{m}$ apart. Find the maximum height attained by the center of mass of the system of particles $A$ and $B$ from the initial position of center of mass of the system. Assume that none of these particles collide with the ground in that duration. Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$.

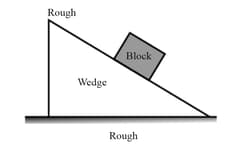
When a block is placed on a wedge as shown in the figure, the block starts sliding down and the wedge also start sliding on ground. All surfaces are rough. The center of mass of (wedge$+$block) system will move,

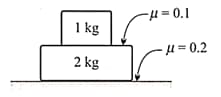
Both the blocks shown in the given arrangement have a horizontal velocity towards right. If $a_{\mathrm{cm}}$ be the subsequent acceleration of the center of mass of the system of blocks, then $a_{\mathrm{cm}}$ equals,