HARD
Earn 100
From the differential equation of linear obtain an expression for acceleration, velocity, and displacement of a particle performing
Important Questions on Oscillations
MEDIUM
One end of a spring of force constant is fixed to a vertical wall and the other to a block of mass resting on a smooth horizontal surface. There is another wall at a distance , from the block. The spring is then compressed by and released. The time taken by the block to strike the other wall is
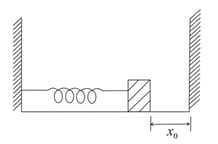
EASY
HARD
HARD
The motion of a mass on a spring, with spring constant is as shown in figure.
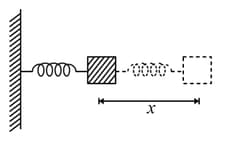
The equation of motion is given by, with .
Suppose that at time the position of mass is and velocity then its displacement can also be represented as where and are
MEDIUM
The position co-ordinates of a particle moving in a coordinate system is given by
and
The speed of the particle is:
HARD
EASY
MEDIUM
EASY
EASY
EASY
EASY
MEDIUM
MEDIUM
HARD
EASY
EASY
MEDIUM
EASY
EASY

