HARD
Earn 100
From the top of a tower of high, Neha observes the angles of depression of the top and foot of another building to be and respectively. Find the height of the building to the nearest whole number (in ). Assume .
50% studentsanswered this correctly
Important Questions on Introduction to Trigonometry
EASY
EASY
Solve for , , if .
MEDIUM
For the given figure and , then _____ and _____
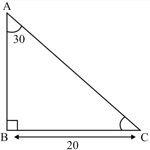
EASY
EASY
EASY
MEDIUM
Find the value of in degrees in .
EASY
EASY
MEDIUM
If is acute, find the value of .
EASY
MEDIUM
MEDIUM
MEDIUM
;
find the value of and
EASY
EASY

