Graphs for two capacitors of capacitances $C_1$ and $C_2$ are shown in figure. The area of plates for both capacitors are same but separation between plates is double for $C_1$ to that of $C_2$. Which of the graph corresponds to $C_1$, and $C_2$ and why?

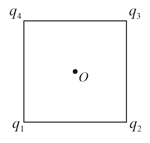
(i) In the given figure, there are four point charges placed at the vertex of a square of side $7 \mathrm{cm}$. If $q_1=+18\mu \mathrm{C}$, $q_2=-24\mu \mathrm{C},q_3=+35\mu \mathrm{C}$ and $q_4=+16\mu \mathrm{C}$, then find the electric potential at the centre $O$ of the square, assume the potential to be zero at infinity.

(ii) An electric field $\overrightarrow{E}=(2\hat{i}+3\hat{j})$ $\mathrm{N} {\mathrm{C}}^{-1}$ exists in the space. If potential at the origin is taken to be $10$ volt, then find the potential at $(2 \mathrm{m},1 \mathrm{m})$.

(i) Two concentric spherical conductors of radius $a$ and $b(b>a)$ inner sphere has $q_1$ charge and outer sphere has $q_2.$ When they are connected by a conducting wire then prove that charge on inner sphere must be zero.
(ii) Find the equivalent capacitance between $A$ and $B.$

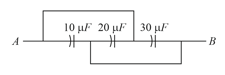
(iii) If the given combination is connected with a battery of emf $200$ volt then find the charge on each capacitor.

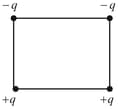
Four point charges $+q,+q,-q,-q$ are placed at the corners of a square as shown in figure. At the centre of the square

In the electric field of a point charge $Q$ which is kept at point $O$, a certain charge is carried from $A$ to $B$ and from $A$ to $C$. If work done from $A$ to $B$ is $W_1$ and from $A$ to $C$ is $W_2$, then (Where $OA=OB=OC$)

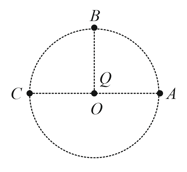
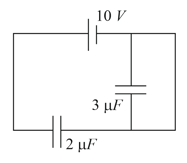
If $V_1$ and $V_2$ are potentials of points $A$ and $B$ respectively then ratio of the charge on capacitor $C_1$ and $C_2$ is $\left(V_1\ne V_2\right)$

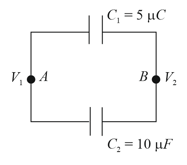
The charge on $2\mu \mathrm{F}$ capacitor as shown in circuit is