EASY

Earn 100

How do you find the direction of angular velocity?

Important Questions on Rotational Dynamics

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

The angular velocity of a particle rotating in a circular orbit

100

times per minute is

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A scooter is going round a circular road of radius

200 m

at a speed of

20 m s^{- 1}

. The angular speed of scooter will be

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A body rotating with an angular speed of

600 rpm

is uniformly accelerated to

1800 rpm

10 \sec .

The number of rotations made in the process is

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A body is moving with constant speed, in a circle of radius

10 m

. The body completes one revolution in

4 s

. At the end of

3 r d

second, the displacement of body (in

m

) from its starting point is:

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A train is moving towards north. At one place it turns towards north-east. Here, we observe that:

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A particle is moving with constant speed in a circular path. When the particle turns by an angle $90 °,$ the ratio of instantaneous velocity to its average velocity is $π : x \sqrt{2} .$ The value of $x$ will be

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A block of

200 g

mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius

20 cm

. If the block takes

40 s

to complete one round, the normal force by the side walls of the groove is:

MEDIUM

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A thin metallic disc is rotating with constant angular velocity about a vertical axis that is perpendicular to its plane and passes through its centre. The rotation causes the free electrons in the disc to redistribute. Assume that, there is no external electric or magnetic field. Then,

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A particle performing

U . C . M .

of radius

\frac{π}{2} m

makes

x

revolutions in time

t

. Its tangential velocity is

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

Two cars of masses

m_{1}

, and

m_{2}

are moving in the circles of radii

r_{1}

and

r_{2}

respectively. Their angular speeds

{}^{'}ω_{1}^{'}

and

{}^{'}ω_{2}^{'}

are such that they both complete one revolution in the same time

t

. The ratio of linear speed of

m_{1}

' to the linear speed of

m_{2}

MEDIUM

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

One end of a straight uniform

1 m

long bar is pivoted on horizontal table. It is released from rest when it makes an angle

30^{o}

from the horizontal (see figure). Its angular speed when it hits the table is given as

\sqrt{n} rad s^{- 1}

, where

n

is an integer. The value of

n

is ____________
Question Image

HARD

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A particle moves such that its position vector

\vec{r} (t) = \cos ω t \hat{i} + \sin ω t \hat{j}

, where

ω

is a constant and

t

is time. Then which of the following statements is true for the velocity

\vec{v} (t)

and acceleration

\vec{a} (t)

of the particle:

MEDIUM

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

A mass $m$ moves in a circle on a smooth horizontal plane with velocity $v_{0}$ at a radius $R_{0}$ . The mass is attached to a string which passes through a smooth hole in plane as shown.

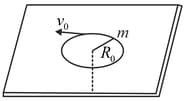
Question Image

The tension in the string is increased gradually and finally $m$ moves in a circle of radius $\frac{R_{0}}{2}$ . The final value of the kinetic energy is:

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

The moon revolved about the earth making a complete revolution in

2.36 Mega second

. Assume that the orbit is circular and has a radius of

385 Mega meter

. What is the magnitude of the acceleration of the moon towards the earth?

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

Calculate the angular velocity and linear velocity of a tip of minute hand of length

10 cm

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

Rohit bought a pizza of a radius of

0.5 m

. A fly lands on the pizza and walks around the edge for a distance of

80 cm

. Calculate the angular distance of the fly?

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

Two cars having masses

m_{1}

and

m_{2}

move in circles of radii

r_{1}

and

r_{2}

respectively. If they complete the circle in equal time, the ratio of their angular speeds

\frac{ω_{1}}{ω_{2}}

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

Define angular displacement, angular velocity and angular acceleration.

EASY

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

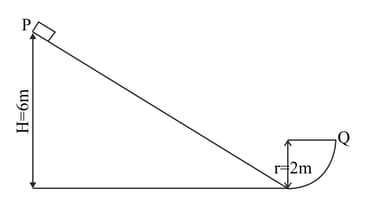
A block of mass $1 kg$ is released from $P$ on a frictionless track which ends in quarter circular track of radius $2 m$ at the bottom. What is the magnitude of radial acceleration and total acceleration of the block when it arrives at $Q$ .

Question Image

HARD

Physics>Mechanics>Rotational Dynamics>Angular Displacement, Angular Velocity and Angular Acceleration

Starting form rest, a particle rotates in a circle of radius

R = \sqrt{2}

m with an angular acceleration α = π/4 rad/s². The magnitude of average velocity of the particle over the time it rotates quarter circle is

How do you find the direction of angular velocity?

Important Questions on Rotational Dynamics

Learn and Prepare for any exam you want !