EASY
Earn 100
How many radioactive series are there?
Important Questions on Nuclear Physics
MEDIUM
MEDIUM
[This question was awarded a bonus and proper correction was made to avoid that]
MEDIUM
In the decay sequence:
and are the particles/ radiation emitted by the respective isotopes. The correct option(s) is/are:
HARD
EASY
MEDIUM
MEDIUM
EASY
The variation of decay rate with number of active nuclei is correctly shown in graph
A 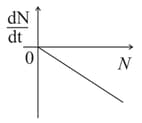
B 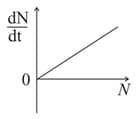
C 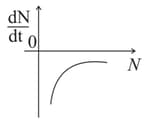
D 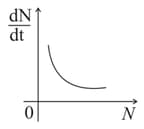
EASY
MEDIUM
MEDIUM
MEDIUM
EASY
MEDIUM
MEDIUM
EASY
EASY
EASY
HARD
MEDIUM
