Identify the function which represents a periodic motion

Two identical coherent sound sources $R$ and $S$ with frequency $f$ are $5 \mathrm{m}$ apart. An observer standing equidistant from the source and at a perpendicular distance of $12 \mathrm{m}$ from the line $RS$ hears maximum sound intensity.

When he moves parallel to $RS$, the sound intensity varies and is a minimum when he comes directly in front of one of the two sources. Then, a possible value of $f$ is close to (the speed of sound is $330 \mathrm{m}/\mathrm{s}$)

The displacement time graph of a particle executing SHM is given in figure: (sketch is schematic and not to scale) 

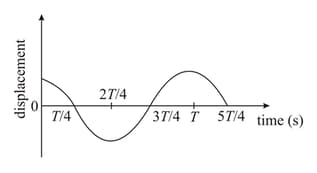
Which of the following statements is/are true for this motion? 

(A) The force is zero at $t=\frac{3T}{4}$
(B) The magnitude of acceleration is maximum at $t=T$
(C) The speed is maximum at $t=\frac{T}{4}$
(D) The $P.E.$ is equal to $K.E.$ of the oscillation at $t=\frac{T}{2}$