If a tunnel is dug inside the earth (not necessarily through the centre) and a ball is dropped at one end of it. Show that the ball will execute SHM. Determine the time period of the ball in terms of and density of earth and also in terms of and radius of the earth

Important Questions on Simple Harmonic Motion
An air chamber having a volume and a cross-sectional area of the neck is into which a ball of mass m can move up and down without friction. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal.
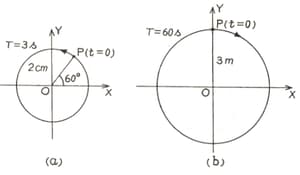
From the adjoining figure obtain the SHM's of Y- projection of the radius vector of the revolving particle in each case
A body of mass executing SHM according to the equation given by meter. Find frequency of oscillation of the particle.
A body of mass executing SHM according to the equation given by meter. Find Initial phase of the particle.
A body of mass executing SHM according to the equation given by meter. Find maximum velocity of the particle
A body of mass executing SHM according to the equation given by Meter. Find Maximum acceleration of the particle.
