If line $AB$ is a secant of the circle where points $A,B$ are on the circle and the line $PQ$ is such that it touches the circle at point $A$, and $\angle BAQ=\angle ACB$ where point $C$ is in the corresponding alternative segment then line $PQ$ is tangent to the circle at point $B$.

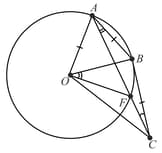
Prove that, “the lengths of the two tangent segments to a circle drawn from an external point are equal”.

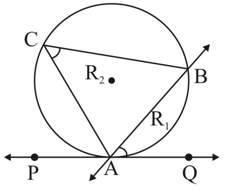
On the circle with center $O$, points $A,B$ are such that $OA = AB$. A point $C$ is located on the tangent at $B$ to the circle such that $A$ and $C$ are on the opposite sides of the line $OB$ and $AB=BC$. The line segment $AC$ intersects the circle again at $F$. Then the ratio $\angle BOF:\angle BOC$ is equal to -

Suppose $S_1 \mathrm{a}\mathrm{n}\mathrm{d} S_2$ are two unequal circles; $AB$ and $CD$ are the direct common tangents to these circles. A transverse common tangent $PQ$ cuts $AB$ in $R$ and $CD$ in $S$. If $AB=10$ units, then $RS$ is -

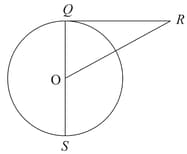
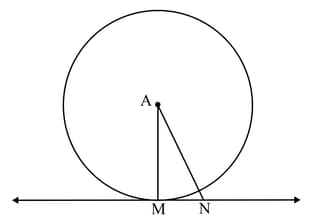
In the following figure, point ‘$A$’ is the centre of the circle. Line $MN$ is tangent at point $M$. If $AN=10 \mathrm{cm}$ and $MN=6 \mathrm{cm}$, determine the radius of the circle.

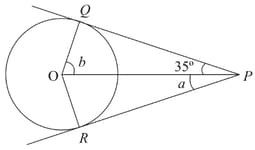
If $\mathrm{PA}$ and $\mathrm{PB}$ are tangents to the circle with centre $\mathrm{O}$ such that $\angle \mathrm{A}\mathrm{P}\mathrm{B}=50°,$ then $\angle \mathrm{O}\mathrm{A}\mathrm{B}$ is equal to

$\mathrm{PQ}$ is a tangent to a circle with center $\mathrm{O}$ at the point $\mathrm{P}$. If $△\mathrm{O}\mathrm{P}\mathrm{Q}$ is an isosceles triangle, then $\mathrm{\angle }\mathrm{O}\mathrm{Q}\mathrm{P}$ is equal to

In the figure, $\mathrm{PQ}$ and $\mathrm{PR}$ are tangents drawn from $\mathrm{P}$ to a circle with centre $\mathrm{O}$. If $\mathrm{\angle }\mathrm{O}\mathrm{P}\mathrm{Q}=35°,$ then

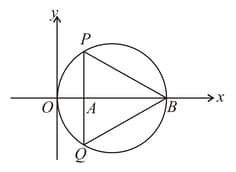
From a point $\mathrm{P}$ which is at a distance $13 \mathrm{c}\mathrm{m}$ from the centre $\mathrm{O}$ of a circle of radius $5 \mathrm{c}\mathrm{m},$ the pair of tangents $\mathrm{PQ}$ and $\mathrm{PR}$ to the circle are drawn. Then the area of the quadrilateral $\mathrm{PQOR}$ is

In figure, $\mathrm{RQ}$ is a tangent to the circle with centre $\mathrm{O}$. If $\mathrm{S}\mathrm{Q}=6 \mathrm{c}\mathrm{m}$ and $\mathrm{Q}\mathrm{R}=4 \mathrm{c}\mathrm{m},$ then $\mathrm{O}\mathrm{R}=$