HARD
Earn 100
If the angle between two lines is and slope of one of the lines is , find the slope of the other line.
Important Questions on Straight Lines
EASY
MEDIUM
MEDIUM
EASY
EASY
HARD
MEDIUM
EASY
EASY
EASY
MEDIUM
EASY
MEDIUM
EASY
What is the slope of the line passing through the points and ? Write the equation of the line.
MEDIUM
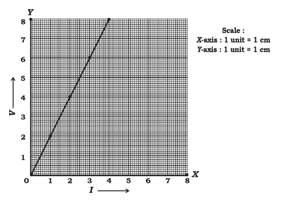
A student, while conducting an experiment on Ohm’s law, plotted the graph according to the given data. Find the slope of the line obtained.
| -axis | ||||
| -axis |
MEDIUM
HARD
MEDIUM

