If the bisector of an angle of a triangle is perpendicular to the opposite side, prove that it is an isosceles triangle. 

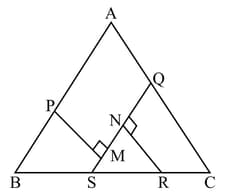
In the figure, in $△ABC, AB=AC=10 \text{cm} \text{and} BC=12 \text{cm}.$ $P \text{and} Q$ are the midpoints of $AB \text{and} AC$ respectively. $PM \text{and} RN$ are perpendiculars on $SQ$. If $BS : SR : RC=1 : 2 : 1$, then the length of $MN$ is:

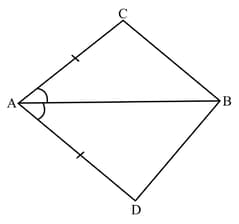
In a quadrilateral $ACBD, AC=AD$ and $AB$ bisects $\angle A$(see figure). Show that $△ABC\cong △ABD$. What can you say about $BC$ and $BD?$     

In the figure given below, $M$ is the mid-point of $AB \text{and} \angle DAB=\angle CBA\text{ and} \angle AMC=\angle BMD$. Then the triangle $ADM$ is congruent to the triangle $BCM$ by______.

In the figure $ABC$ is an equilateral triangle with side $14$ cm. $AX=\frac{1}{3}AB, BY=\frac{1}{3}BC \text{and} CZ=\frac{1}{3}AC$. What is the area (in ${\mathrm{cm}}^2$ ) of $△PQR$?

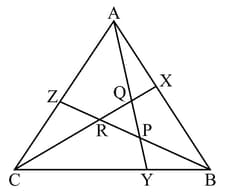
From the information shown in the figure, state the test assuring the congruence of $△ABC$ and $\Delta PQR$. Write the remaining congruent parts of the triangles.

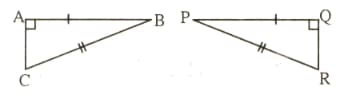
In the adjoining figure, $\mathrm{X}$ and $\mathrm{Y}$ are respectively two points on equal sides $\mathrm{AB}$ and $\mathrm{AC}$ of $∆\mathrm{ABC}$ such that  $\mathrm{AX}=\mathrm{AY}$. Prove that $\mathrm{CX}=\mathrm{BY}$.

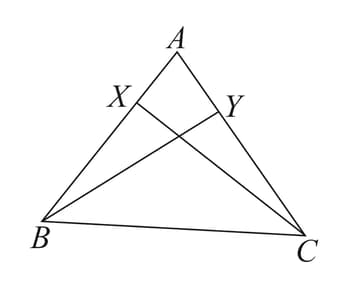
In the given figure, if $x=y$ and $\mathrm{AB}=\mathrm{CB}$, then prove that $\mathrm{AE}=\mathrm{CD}$.

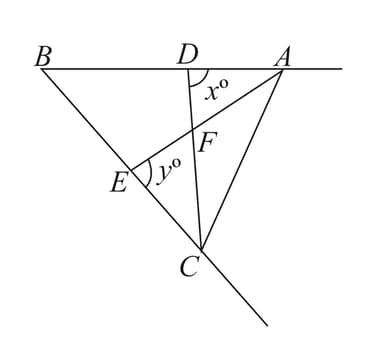
In $△ABC$ and $△DEF$, three equality relations between same parts are: $AB=ED$, $\angle B=\angle D$, $BC=DF$, then which of the following congruence conditions applies?

In figure, $\mathrm{seg} AB\cong \mathrm{seg} CB$ and $\mathrm{seg} AD\cong \mathrm{seg} CD$. 

Prove that $△ABD\cong △CBD$.

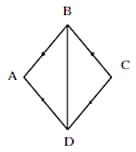
In $∆\mathrm{ABC}, \mathrm{D}$ is the midpoint of $\mathrm{BC}$. If $\mathrm{DL}\perp \mathrm{AB}$ and $\mathrm{DM}\perp \mathrm{AC}$ such that $\mathrm{DL}=\mathrm{DM}$, prove that $\mathrm{AB}=\mathrm{AC}$.

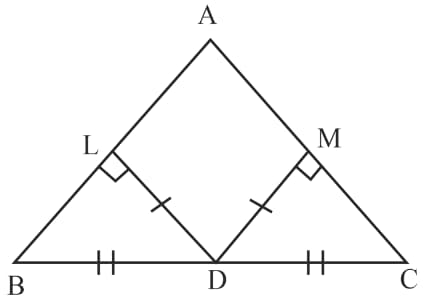
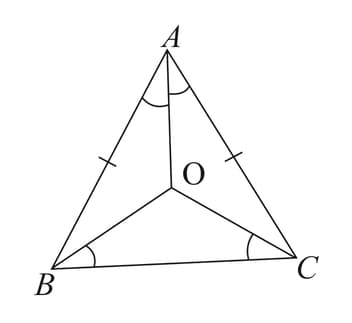
In $∆\mathrm{ABC}, \mathrm{AB}=\mathrm{AC}$ and the bisectors of $\angle \mathrm{B}$ and $\angle \mathrm{C}$ meet at a point $\mathrm{O}$. prove that $\mathrm{BO}=\mathrm{CO}$ and the ray $\mathrm{AO}$ is the bisector of $\angle \mathrm{A}$.