Imagine a short dipole at the centre of a spherical surface. If the magnitude of the electric field at a certain point on the surface of the sphere is $10 \mathrm{N} {\mathrm{C}}^{-1},$ Then which of the following cannot be the magnitude of the electric field anywhere on the surface of the sphere?

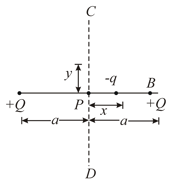
In arrangement shown in figure, two positive charges, $+Q$ each are fixed. Mark the correct statement (s) regarding a third charged particle $q$ placed at the midpoint $P$ that can be displaced along or perpendicular to the line connecting the charges.

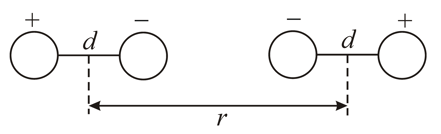
We have two electric dipoles. Each dipole consists of two equal and opposite point charges at the ends of an insulating rod of length $d.$ The dipoles sit along the $x$-axis a distance $r$ apart, oriented as shown in the figure.
Their separation $r\gg d.$ The dipole on the left:

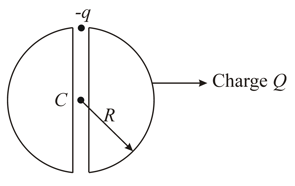
In a uniformly charged dielectric sphere, a very thin tunnel has been made along the diameter as shown in figure. A charge particle $-q$ having mass $m$ is released from rest at one end of the tunnel. For the situation described, mark the correct statement(s). (Neglect gravity.)

Consider two identical charges placed distance $2d$ apart, along the $x$-axis (see figure). The equilibrium of a positive test charge placed at point $O$ midway between them is,

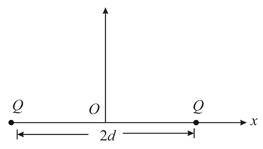
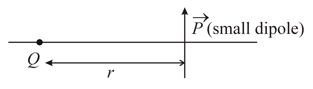
For the situation shown in the figure (assume $r\gg$the length of the dipole) mark out the correct statement(s).