MEDIUM
Earn 100
Imagine a uniform wire of length '' suspended from the ceiling whose young's modulus of elasticity increases linearly from yo at the bottom to yo at the top. If is the area of cross- section and be the load applied at its bottom then (neglect change in area of cross-section).
(a)Total elongation of the wire is (if rope is light)
(b)The strain energy developed in the wire is (if rope is light)
(c)Tension is maximum at the top of rope and equal to (if is linear density of rope)
(d)Tension is maximum at the bottom of rope and equal to (if is linear density of rope)
50% studentsanswered this correctly
Important Questions on Properties of Solid and Liquid
MEDIUM
EASY
MEDIUM
EASY
EASY
MEDIUM
MEDIUM
MEDIUM
HARD
EASY
HARD
(gravitational acceleration)
EASY
MEDIUM
EASY
HARD
String of unstretched length is stretched by applying a force at the mid-point such that the segments and make an angle with as shown in the figure. The string may be considered as an elastic element with a force to elongation ratio . The force is given by
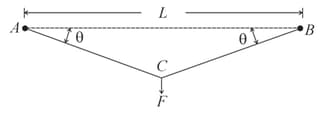
MEDIUM
HARD
MEDIUM
= Young's modulus of the material of rod, coefficient of linear expansion
HARD

