In Young's double-slit experiment, the red light of wavelength $6000 \stackrel{\circ }{\mathrm{A}}$ is used and the $n^{\mathrm{th}}$ bright fringe is obtained at a point $P$ on the screen. Keeping the same setting, the source of light is replaced by the green light of wavelength $5000 \stackrel{\circ }{\mathrm{A}}$ and now $(n+1{)}^{\mathrm{th}}$ bright fringe is obtained at the point $P$ on the screen. The value of $n$ is 

In Young's double-slit experiment, if the distance between two slits is equal to the wavelength of used light. Then the maximum number of bright fringes obtained on the screen will be 

A mixture of light consisting of wavelength $590 \mathrm{nm}$ and an unknown wavelength illuminates Young's double-slit and gives rise to two overlapping interference patterns on the screen. The central maximum of both lights coincide. Further, it is observed that the third bright fringe of known light coincides with the $4^{\mathrm{th}}$ bright fringe of the unknown light. From this data, the wavelength of the unknown light is 

The monochromatic green light of wavelength $5\times {10}^{-7} \mathrm{m}$ illuminates a pair of slits $1 \mathrm{mm}$ apart. The separation of bright lines on the interference pattern formed on a screen $2 \mathrm{m}$ away is

In the figure is shown Young's double-slit experiment. $Q$ is the position of the first bright fringe on the right side of $O$. $P$ is the ${11}^{\mathrm{th}}$ fringe on the other side, as measured from $Q$. If the wavelength of the light used is $6000\times {10}^{-10} \mathrm{m}$, then $S_{1}B$ will be equal to 

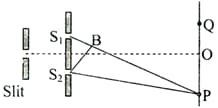
Two coherent sources $P$ and $Q$ produce interference at a point $A$ on the screen where there is a dark band which is formed between $4^{\mathrm{th}}$ bright band and $5^{\mathrm{th}}$ bright band. The wavelength of light used is $6000 \stackrel{\circ }{\mathrm{A}}$. The path difference between $PA$ and $QA$ is

A beam of light of $\lambda =600 \mathrm{nm}$ from a distant source falls on a single slit $1 \mathrm{mm}$ wide and the resulting diffraction pattern is observed on a screen $2 \mathrm{m}$ away. The distance between the first dark fringes on either side of the central bright fringe is

A fringe width of a certain interference pattern is $\beta =0.002 \mathrm{cm}$. What is the distance of $5^{\mathrm{th}}$ order minima from central maxima?

Two slits separated by a distance of $1 \mathrm{mm}$ are illuminated with light of wavelength $4\times {10}^{-7} \mathrm{m}$. The interference fringes are observed on a screen placed $1 \mathrm{m}$ from the slits. The distance between the fourth dark and sixth bright fringe on the same side is equal to