In a , is drawn perpendicular to . Prove that .

Important Questions on Similar Triangles
In a right-angled triangle, prove that the square of the hypotenuse is equal to the sum of the squares of the other two sides. Using the theorem, determine the length of in terms of and .
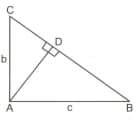
is a right angle triangle, right-angled at . If is the length of the perpendicular from to and have the usual meaning, then prove that .
is a right angle triangle, right-angled at . If is the length of the perpendicular from to and have the usual meaning, then prove that .
A long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point high. If the foot of the ladder is moved towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
For going to a city from city , there is a route via city such that , and . It is proposed to construct a highway which directly connects the two cities and . Find how much distance will be saved in reaching city from city after the construction of the highway.
In , such that lies on . If , , and , prove that .
In a quadrilateral , . Prove that .
In a right-angled triangle, the bisector of the right angle divides the hypotenuse in the ratio . If in ratio the hypotenuse is divided by the altitude dropped from the vertex of the right angle then find .
