EASY
Earn 100
In a YDSE set up in air, the fringe width is If the whole set up is now immersed inside a liquid of refractive index , the fringe width will become , find
50% studentsanswered this correctly
Important Questions on Wave Optics
HARD
HARD
MEDIUM
MEDIUM
MEDIUM
MEDIUM
Using monochromatic light of wavelength , an experimentalist sets up the Young's double slit experiment in three ways as shown.
If she observes that , the wavelength of light used is :
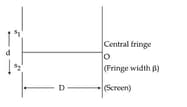
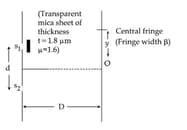
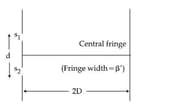
HARD
MEDIUM
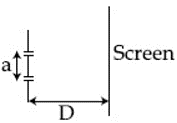
MEDIUM
MEDIUM
HARD
HARD
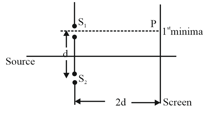
EASY
EASY
MEDIUM
HARD
MEDIUM
MEDIUM
MEDIUM
EASY

