In a survey on pet ownership, $36\%$ of the participants own a cat, $20\%$ own a hamster but not a cat, and $8\%$ own a hamster and a cat. What percentage of the participants owns neither a hamster nor a cat?

A garage repaired $132$ vehicles last month. The number of vehicles that required electrical $\left(E\right)$, mechanical $\left(M\right)$ and bodywork $\left(B\right)$ repairs are given in the diagram opposite.

Find the probability that a randomly selected vehicle required mechanical or bodywork repairs.

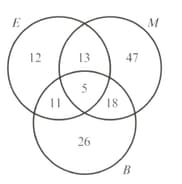
A garage repaired $132$ vehicles last month. The number of vehicles that required electrical $\left(E\right)$, mechanical $\left(M\right)$ and bodywork $\left(B\right)$ repairs are given in the diagram opposite.

Find the probability that a randomly selected vehicle required no bodywork repairs.

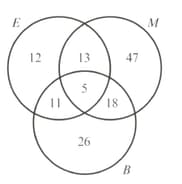
A garage repaired $132$ vehicles last month. The number of vehicles that required electrical $\left(E\right)$, mechanical $\left(M\right)$ and bodywork $\left(B\right)$ repairs are given in the diagram opposite.

Find the probability that a randomly selected vehicle required exactly two types of repair.

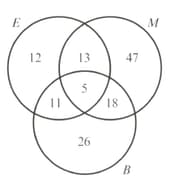
The $100$ students at a technical college must study at least one subject from Pure Mathematics $\left(P\right)$, Statistics $\left(S\right)$ and Mechanics $\left(M\right)$. The numbers studying these subjects are given in the diagram opposite.

Who does the number $17$ in the diagram refer to?

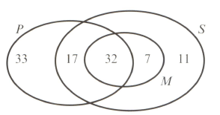
The $100$ students at a technical college must study at least one subject from Pure Mathematics $\left(P\right)$, Statistics $\left(S\right)$ and Mechanics $\left(M\right)$. The numbers studying these subjects are given in the diagram opposite.

Find the probability that a randomly selected student studies: Pure Mathematics or Mechanics.

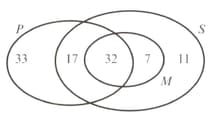
The $100$ students at a technical college must study at least one subject from Pure Mathematics $\left(P\right)$, Statistics $\left(S\right)$ and Mechanics $\left(M\right)$. The numbers studying these subjects are given in the diagram opposite.

Find the probability that a randomly selected student studies exactly two of these subjects.

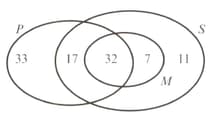
The $100$ students at a technical college must study at least one subject from Pure Mathematics $\left(P\right)$, Statistics $\left(S\right)$ and Mechanics $\left(M\right)$. The numbers studying these subjects are given in the diagram opposite.

List the three subjects in ascending order of popularity.

Events $X$ and $Y$ are such that $\mathrm{P}\left(X\right)=0.5, \mathrm{P}\left(Y\right)=0.6$ and $\mathrm{P}(X\cap Y)=0.2$.

State, giving a reason, whether events $X$ and $Y$ are mutually exclusive.