In a triangle OAB, E is mid-point of OB and D is a point on AB such that AD : DB = 2 : 1. If OD and AE intersect at P, determine the ratio OP : PD, using vector methods.

ABCD is a parallelogram. P and Q are points on the sides AB and AD respectively such that AB = 2AP and AD = 3AQ. Show that the diagonal AC divides PQ in the ratio 3 : 2 and is itself divided by PQ in the ratio 1 : 4.

Prove by vector method that the line segment joining the midpoints of the diagonals of a trapezium is parallel to the parallel sides and equal to half of their difference.

In a triangle ABC, D and E are points on BC and AC respectively, such that BD = 2 DC and AE = 3 EC. Let P be the point of intersection of AD and BE. Find BP/PE using vector method.

If $\overrightarrow{a}·\overrightarrow{b}\ne 0$, find the vector$\overrightarrow{r}$ which satisfies the equations :$\overrightarrow{r}\times \overrightarrow{b}=\overrightarrow{c}\times \overrightarrow{b}$ and $\overrightarrow{r}·\overrightarrow{a}=0$

If$\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}$ are unit vectors such that$\overrightarrow{a}·\overrightarrow{b}=\overrightarrow{a}·\overrightarrow{c} =0$ and the angle between $\overrightarrow{b}$ and $\overrightarrow{c}$ is $\frac{\mathrm{\pi }}{3}$,  then prove that$\overrightarrow{a}=\pm 2( \overrightarrow{b} \times \overrightarrow{c})$ .

If O and H are respectively the circumcentre and orthocentre of a triangle whose vertices are the points A, B and C with position vectors $\overrightarrow{a}, \overrightarrow{b}$ and $\overrightarrow{c}$ respectively with reference to O as origin, then prove that $\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{OH}$ .

If 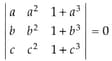 and the vectors $\overrightarrow{A}=(1, a, a^2)$, $\overrightarrow{B}=(1, b, b^2)$, $\overrightarrow{C}=(1, c, c^2)$ are non-coplanar, then prove that $abc = -1$.

Show that the points with position vectors $2\hat{i}+6\hat{j}+3\hat{k}, \hat{i}+2\widehat{ j}+\hat{k}$  and $3\hat{i}+10\hat{j}+5\hat{k}$ are collinear.