In a uniform electric field $E$ if we consider an imaginary cubical closed surface of side $a$, then find the net flux through the cube ?

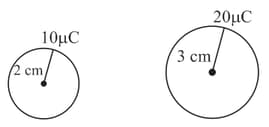
Find the flux of the electric field through a spherical surface of radius $R$ due to a charge of $8.85 \times {10}^{–8} \mathrm{C}$ at the centre and another equal charge at a point $3R$ away from the centre (Given, ${\mathrm{\epsilon }}_0 = 8.85 \times {10}^{–12}$ units).

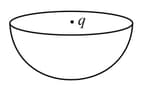
A charge $\mathrm{q}$ is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and the Gauss’s law, find the electric flux due to this charge through the given surface.

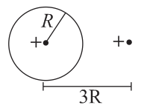
The figure shows two conducting spheres separated by a large distance and of radius $2 \mathrm{cm}$ and $3 \mathrm{cm}$ containing charges $10 \mathrm{\mu C}$ and $20 \mathrm{\mu C}$, respectively. When the spheres are connected by a conducting wire, find out the following

$\left(\mathrm{i}\right)$ The ratio of the final charges.

$\left(\mathrm{ii}\right)$ Final charge on each sphere. 

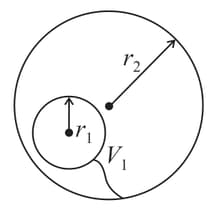
$\left(\mathrm{iii}\right)$ The ratio of final charge densities.

Two concentric hollow conducting spheres of radius $a$ and $b\left(b>a\right)$ contains charges $Q_{\mathrm{a}}$ and $Q_{\mathrm{b}}$, respectively. If they are connected by a conducting wire then find out 

$\left(\mathrm{i}\right)$ Final charges on inner and outer spheres.

$\left(\mathrm{ii}\right)$ The heat produced during the process.

There are two concentric metal shells of radii $r_1$ and $r_2\left(>r_1\right)$. If initially, the outer shell has a charge $q$ and the inner shell is having zero charges and then the inner shell is grounded. Find

$\left(\mathrm{i}\right)$ Charge on the inner surface of the outer shell.

$\left(\mathrm{iii}\right)$ The charge is flown through the wire in the ground.

A metal sphere of radius $r_1$ charged to potential $V_1$ is then placed in a thin-walled uncharged conducting spherical shell of radius $r_2$. Determine the potential acquired by the spherical shell after it has been connected for a short time to the sphere by a conductor.