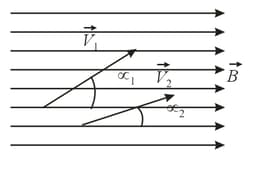
In a uniform magnetic field there are two charged particles moving with velocities $v_1$ and $v_2$ and carrying equal charges, with $\left|v_1\right|=\left|v_2\right|=v$. The velocity of one particle forms an angle ${\alpha }_1$ with the direction of the field, while the other velocity forms an angle ${\alpha }_2$. In what parameters does the motion of one particle differ from that of the other? Determine which of the parameters is greater for which particle.

             

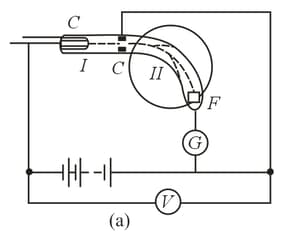
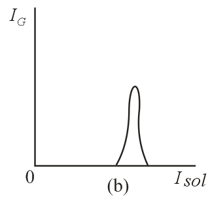
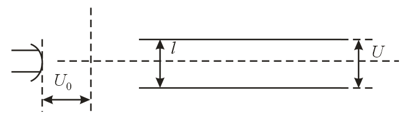
The device shown in Figure is commonly used to measure the charge-to-mass ratio of the electron. The electrons that leave the cathode $C$ are accelerated by an electric field that exists in the space between the cathode and the anode $A$. A fraction of electrons fly through the hole in the anode. These electrons, leaving region $I$ of the device, fly into the region where there is no electric field. In this region the electrons are deflected from a straight line via a magnetic field directed perpendicularly to the plane of the drawing. This field is generated by two solenoids. The region $II$ where the trajectory of the electrons is bent lies between these two solenoids. By increasing the current flowing through the two solenoids connected in series we can direct the electrons into a Faraday cylinder $F$, with a galvanometer $G$ registering the resulting current. Any further increase in the solenoid current results in a drop in the current flowing through $G$, since the electrons begin to move along a circle of a smaller radius. The dependence of the galvanometer current on the solenoid current is illustrated by the curve in Figure The following quantities are known in measurements: the potential difference $U$ between anode and cathode, the curvature radius $R$ of the axial line of region $II$ (assuming that the majority of electrons deflected by the magnetic field travel along this line), the number of turns $N_0$ per unit length of solenoid, and the solenoid current $I$ at which the galvanometer current is maximal. How to determine the charge-to-mass ratio of the electron knowing the values of these quantities?

A charged particle of mass $m$ and charge $Q$ has acquired a certain velocity by passing through a potential difference $U_0$. With this velocity it flies into the field of a parallel-plate capacitor, with the distance between the plates being $l$, the potential difference being $U$. The velocity of the particle is directed parallel to the plates. Where should the magnetic field that makes the particle move along a straight line in the capacitor be directed and what should its value be (the induction $B$)?

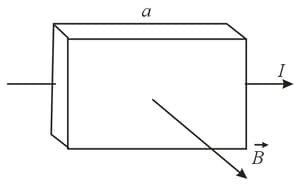
A direct current $I$ is flowing through a plane in the direction designated by an arrow. The plate is placed in a transverse magnetic field $B$. As a result of the Hall effect there appears a transverse potential difference. What is the sign of the potential at point $a$ if the plate is made of metal and if the plate is an $n$-type or $p$-type semiconductor?

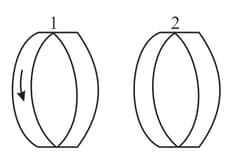
Two contours are positioned in such a manner that their planes are parallel to each other. Contour $1$ carries a current whose direction is designated by an arrow. The contours move in relation to one another, but their planes remain parallel in the process. What is the direction of the current induced in contour $2$ when the contours are moved toward each other or away from each other?

A spiral made from elastic wire is connected to a DC source. The spiral is stretched. Will the current flowing in the spiral become greater or smaller in the stretching process than the initial current or will it remain unchanged?

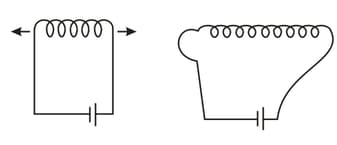
A solenoid carrying a current supplied by a DC source with a constant emf contains an iron core inside it. How will the current change when the core is pulled out of the solenoid: will it increase, decrease, or remain the same?

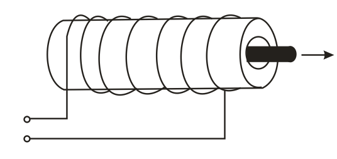
Two identical inductances carry currents that vary with time according to linear laws. In which of the two inductances is the self-induction emf greater? Will the values or signs of the self-induction emf's change if the currents begin to increase in the opposite direction after they pass through zero (with the linear laws retained in the process)?

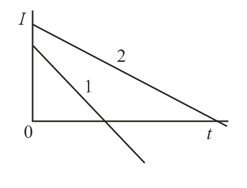
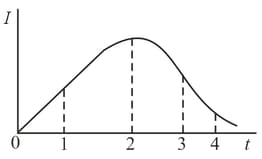
A current that varies with time according to a law depicted graphically in the figure passes through an induction coil. In which of the moments denoted in the figure will the self-induction emf be maximal (the inductance of the coil remains unchanged in the process)?