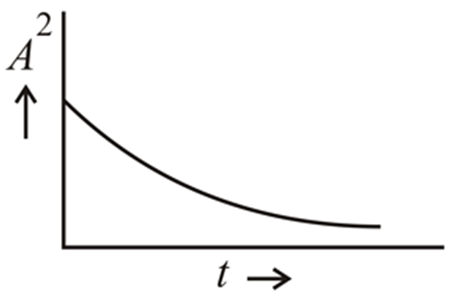
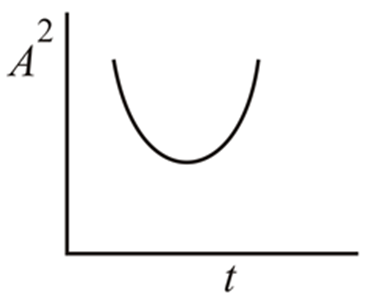
In an experiment to find the loss of energy with respect to time in the case of a swinging simple pendulum, the graph between the square of amplitude and time is best represented by

A pendulum with the time period of $1 \mathrm{s}$ is losing energy due to damping. At a certain time, its energy is $45 \mathrm{J}$. If after completing $15$ oscillations its energy has become $15 \mathrm{J}$, then its damping constant (in ${\mathrm{s}}^{-1}$) will be

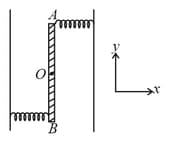
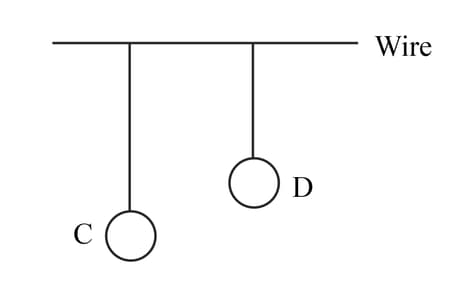
Two pendulums $C$ and $D$ are suspended from a wire as shown in the given figure. Pendulum $C$ is made to oscillate by displacing it from its mean position. It is seen that $D$ also starts oscillating. If the length of $D$ is made equal to $C$, then what difference will you notice in the oscillations of $D$? 

The amplitude of a simple pendulum, oscillating in air with a small spherical bob, decreases from 10 cm to 8 cm in 40 seconds. Assuming that Stokes law is valid, and ratio of the coefficient of viscosity of air to that of carbon dioxide is 1.3, the time in which amplitude of this pendulum will reduce from 10 cm to 5 cm in carbondioxide will be close to (ln 5 = 1.601, ln 2 = 0.693).