EASY

Earn 100

In case of simple harmonic motion, the restoring force is proportional to the .

62.5% studentsanswered this correctly

Important Questions on Oscillations

HARD

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

For a simple pendulum, a graph is plotted between its kinetic energy (K.E.) and potential energy (P.E.) against its displacement d. which one of the following represents these correctly? (graphs are schematic and not drawn to scale)

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A body of mass

M

and charge

q

is connected to a spring of spring constant

k

. It is oscillating along

x

-direction about its equilibrium position in the horizontal plane, taken to be at

x = 0

, with an amplitude

A

. An electric field

E

is applied along the

x

-direction. Which of the following statements is correct?

HARD

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A hollow sphere of radius

R

is suspended from a thin rod. If the sphere is twisted by a small angle about the wire axis and released, simple harmonic oscillation (SHM) will ensure with a period of

τ_{1}

. Now, if the hollow sphere is replaced by a solid sphere of radius and mass equal to that of a hollow sphere, the SHM will have a period

τ_{2}

. The ratio of time periods

(τ_{1} / τ_{2})

HARD

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A particle executes simple harmonic motion with an amplitude of

5 cm

. When the particle is at

4 cm

from the mean position, the magnitude of its velocity in

SI

units is equal to that of its acceleration. Then, its periodic time in seconds is:

EASY

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A mass

M

is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes

S . H . M .

of period

T

. If the mass is increased by

m

, the time period becomes

\frac{5 T}{3} .

What is the ratio

(\frac{M}{m})

HARD

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A cylindrical plastic bottle of negligible mass is filled with

310 ml

of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic motion at angular frequency

ω .

If the radius of the bottle is

2 .5 cm

then

ω

is close to:

(

density of water

= 10^{3} kg m^{- 3})

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A rod of mass

M

and length

2 L

is suspended at its middle by a wire. It exhibits torsional oscillations. If two masses, each of mass

m

, are attached at a distance

L / 2

from its centre on both sides, it reduces the oscillation frequency by

20 %

. The value of ratio

m / M

is close to

HARD

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

Two vectors

\vec{A}

and

\vec{B}

are defined as

\vec{A} = a \hat{i}

and

\vec{B} = a (\cos ω t \hat{i} + \sin ω t \hat{j})

, where a is a constant and

ω = \frac{π}{6} rad s^{- 1} .

|\vec{A} + \vec{B}| = \sqrt{3} |\vec{A} - \vec{B}|

at time

t = τ

for the first time, the value of

τ

in seconds, is_______

HARD

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

State the differential equation of linear simple harmonic motion.

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A body of mass

1 kg

is made to oscillate on a spring of force constant

15 N / m

. Calculate the frequency of vibrations.

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

Two light identical springs of spring constant

k

are attached horizontally at the two ends of a uniform horizontal rod

A B

of length

l

and mass

m .

The rod is pivoted at its center 'O' and can rotate freely in horizontal plane. The other ends of the two springs are fixed to rigid supports as shown in figure. The rod is gently pushed through a small angle and released. The frequency of resulting oscillation is:
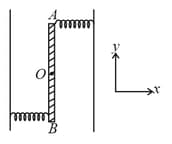
Question Image

HARD

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A block of mass

2 M

is attached to a massless spring with spring-constant

k .

This block is connected to two other blocks of masses

M

and

2 M

using two massless pulleys and strings. The accelerations of the blocks are

a_{1}, a_{2}

and

a_{3}

as shown in figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is

x_{0} .

Which of the following option(s) is/are correct?
[

g

is the acceleration due to gravity. Neglect friction]

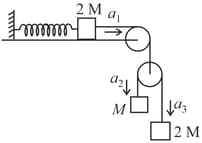
Question Image

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A particle is executing simple harmonic motion

(S H M)

of amplitude

A,

along the

x

-axis, about

x = 0 .

When its potential Energy

(P E)

equals kinetic energy

(K E),

the position of the particle will be:

HARD

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A block with mass

M

is connected by a massless spring with stiffness constant

k

to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude

A

about an equilibrium position

x_{0}

. Consider two cases : (i) when the block is at

x_{0}

and (ii) when the block is at

x = x_{0} + A

. In both the cases, a particle with mass

m (< M)

is softly placed on the block after which they stick to each other. Which of the following statement(s) is(are) true about the motion after the mass

m

is placed on the mass

M

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

The position co-ordinates of a particle moving in a $3 D$ coordinate system is given by

$x = a \cos ω t$

$y = a \sin ω t$

and $z = a ω t$

The speed of the particle is:

EASY

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A particle is executing a simple harmonic motion. Its maximum acceleration is

α

and maximum velocity is

β

. Then, its time period of vibration will be:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A spring - block system is resting on a frictionless floor as shown in the figure. The spring constant is

2.0 N m^{- 1}

and the mass of the block is

2 .0 kg

. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass

1.0 kg

moving with a speed of

2 .0 m s^{- 1}

collides elastically with the first block. The collision is such that the

2.0 kg

block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is _________.

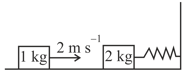
Question Image

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A body of mass

1 kg

is made to oscillate on a spring of force constant

15 N / m

. Calculate the angular frequency

MEDIUM

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

A simple harmonic oscillator of frequency

1 Hz

has a phase of

1

radian. By how much should the origin be shifted in time so as to make the phase of the oscillator vanish. (time in seconds).

EASY

Physics>Oscillations and Waves>Oscillations>Force Law for Simple Harmonic Motion

For a particle performing linear SHM, its average speed over one oscillation is (

A =

amplitude of S.H.M.,

n =

frequency of oscillation)

In case of simple harmonic motion, the restoring force is proportional to the .

Important Questions on Oscillations

Learn and Prepare for any exam you want !