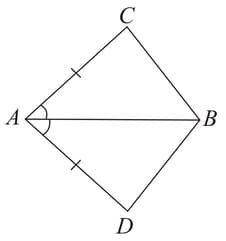
In quadrilateral $ACBD, AC=AD$ and $AB$ bisects $\angle A$ (see given figure). If $△ABC\cong △ABD.$ Is $BC=$$BD$ (Yes/No) ?

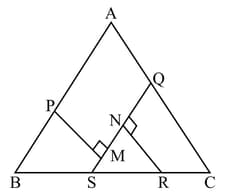
In the figure, in $△ABC, AB=AC=10 \text{cm} \text{and} BC=12 \text{cm}.$ $P \text{and} Q$ are the midpoints of $AB \text{and} AC$ respectively. $PM \text{and} RN$ are perpendiculars on $SQ$. If $BS : SR : RC=1 : 2 : 1$, then the length of $MN$ is:

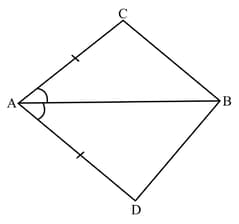
In a quadrilateral $ACBD, AC=AD$ and $AB$ bisects $\angle A$(see figure). Show that $△ABC\cong △ABD$. What can you say about $BC$ and $BD?$     

In the figure given below, $M$ is the mid-point of $AB \text{and} \angle DAB=\angle CBA\text{ and} \angle AMC=\angle BMD$. Then the triangle $ADM$ is congruent to the triangle $BCM$ by______.

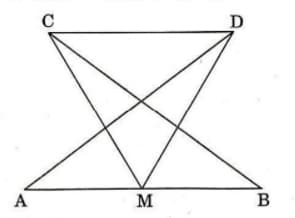
In the figure $ABC$ is an equilateral triangle with side $14$ cm. $AX=\frac{1}{3}AB, BY=\frac{1}{3}BC \text{and} CZ=\frac{1}{3}AC$. What is the area (in ${\mathrm{cm}}^2$ ) of $△PQR$?

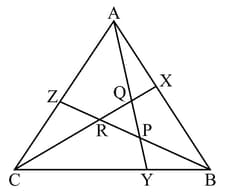
In the given figure, $ABCD$ is a quadrilateral in which $AD=BC$ and $\angle ADC=\angle BCD$. Show that the points $A, B, C, D$ lie on a circle.

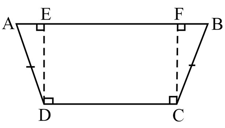
Observe the information shown in pairs of triangles given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.

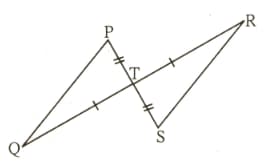
From the information shown in the figure.,

 In $△PTQ=△STR$

 $\angle PTQ=\angle STR$ ..... vertically opposite angles

 seg $TQ\cong$ seg $TR$

 $△PTQ\cong △STR$....._____ test

$\angle TPQ\cong$ _____ .....corresponding angles of congruent triangles.

_____ $\cong \angle TRS$ .....corresponding angles of congruent triangles.

seg $PQ\cong$ _____ ..... corresponding sides of congruent triangles.

In the adjoining figure, $\mathrm{BM}\perp \mathrm{AC}$ and $\mathrm{DN}\perp \mathrm{AC}$. If $\mathrm{BM}=\mathrm{DN}$, prove that $\mathrm{AC}$ bisects $\mathrm{BD}$.

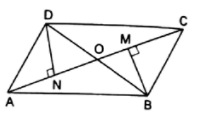
Diagonals of parallelogram $ABCD$ intersect at $O$ as shown in Fig. $XY$contains $O$, and $X,$$Y$are points on opposite sides of the parallelogram. Give reasons for the following:

$∆BOY\cong ∆DOX$.

Now, state if $XY$ is bisected at $O$.

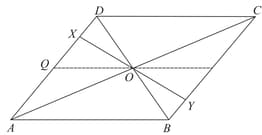
In figure, segment $PT$ is the bisector of $\angle QPR$. A line through $R$ intersects ray $QP$ at point $S$ and $RS\parallel PT$. Prove that $PS=PR$.

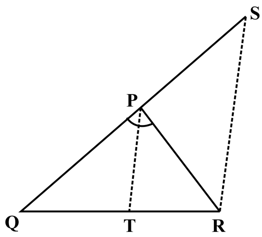
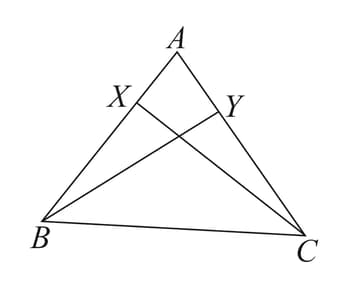
In the adjoining figure, $\mathrm{X}$ and $\mathrm{Y}$ are respectively two points on equal sides $\mathrm{AB}$ and $\mathrm{AC}$ of $∆\mathrm{ABC}$ such that  $\mathrm{AX}=\mathrm{AY}$. Prove that $\mathrm{CX}=\mathrm{BY}$.